При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r 0 заменяют расчетным эквивалентным источником ЭДС или источником тока.
Рис. 1.14
Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r 0, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.
Для данной цепи запишем соотношение по второму закону Кирхгофа
E = U + Ir 0 или E = U − Ir 0. (1.10)
Эта зависимость напряжения U на зажимах реального источника от тока I определяется его вольт-амперной или внешней характеристикой (рис. 1.15). Уменьшение напряжения источника U при увеличении тока нагрузки I объясняется падением напряжения 
на его внутреннем сопротивлении r 0.
Рис. 1.18 Рис. 1.19
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока I 0, замыкающегося в цепи источника тока.
В идеальном источнике тока r 0>> R н. В этом случае можно считать, что при изменении сопротивления нагрузки R нпотребителя I 0≈0, а I ≈ I к. Тогда из выражения (1.11) следует, что вольт-амперная характеристика I (U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I = I к= E / r 0 (рис. 1.19).
При сравнении внешних характеристик источника ЭДС (рис. 1.15) и источника тока (рис. 1.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.
Ток в нагрузке R н для схем источника ЭДС (рис. 1.14) и источника тока (рис. 1.17) одинаков и равен
Для схемы (рис. 1.14) это следует из закона Ома, т.к. при последовательном соединении сопротивления r 0 и R н складываются. В схеме (рис. 1.17) ток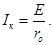 
распределяется обратно пропорционально сопротивлениям r 0 и R н двух параллельных ветвей. Ток в нагрузке R н
т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 1.17) эквивалентна схеме источника ЭДС (рис. 1.14) в отношении энергии, выделяющейся в сопротивлении нагрузки R н, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.
Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r 0 и величиной электродвижущей силы E.
В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.
Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 1.20).
Рис. 1.20
Для этой цепи на основании второго закона Кирхгофа можно записать
E 1+ E 2+ E 3= I (r 01+ r 02+ r 03+ R н),
откуда
Таким образом, электрическая цепь на рис. 1.20 может быть заменена цепью с эквивалентным источником питания (рис. 1.21), имеющим ЭДС E э и внутреннее сопротивление r э.
Рис. 1.21 Рис. 1.22
При параллельном соединении источников (рис. 1.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U на выводах всех источников. Для электрической цепи на рис. 1.22 можно записать следующие уравнения:
I = I 1+ I 2+ I 3; P = P 1+ P 2+ P 3= UI 1+ UI 2+ UI 3= UI.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей. На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.
Делитель напряжения
Для уменьшения значения входного (питающего) напряжения используют делитель напряжения на резисторах. В нём, выходное напряжение Uвых зависит от значения входного (питающего) напряжения Uвх и значения сопротивления резисторов. Делитель напряжения – наиболее часто применяемое соединение резисторов. Например, переменный резистор, используемый в качестве регулятора громкости Ваших компьютерных колонок, является делителем напряжения с изменяемыми сопротивлениями плеч, где он выполняет роль ограничителя амплитуды входного сигнала.
Так как, сопротивление нагрузки влияет на выходное напряжение Uвых делителя, для обеспечения точности делителя напряжения, необходимо выполнять правило (2):
Значение резистора R2 должно быть приблизительно на два порядка меньше (в 100 раз) сопротивления нагрузки подключаемой к выходу делителя.
Используя закон Ома, и пренебрегая малым током нагрузки, делитель напряжения можно описать соотношением:
Преобразовывая указанную формулу, можно определить:
1. Выходное напряжение Uвых по известным значениям входного напряжения Uвх и сопротивлений резисторов R1, R2:
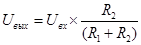
2. Входное напряжение делителя Uвх, по известным значениям выходного напряжения Uвых и сопротивлений резисторов R1, R2:
3. Значение R1 по известным значениям входного напряжения Uвх, выходного напряжения Uвых и сопротивления резистора R2:
4. Значение R1 и R2 по известным значениям входного напряжения Uвх, выходного напряжения Uвых и входного (общего) сопротивления делителя Rобщ, где Rобщ = R1 + R2:
Делитель тока
Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.
Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют "шунтом", так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра - ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам).
Изобразим цепь делителя тока:
На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.
Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов:
, 
, 
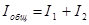Выведем закон Ома для этой цепи. Его можно записать в следующем виде:
Преобразовывая указанные формулы, можем определить:
1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2:
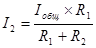
2. Расчитать шунт R2 в цепи измерительного прибора, при известных: внутреннем сопротивлении R1, максимальном токе обмотки катушки прибора I1 и максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:
