Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем.
При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).
|
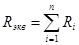или 
(1.32)
Это следует из II закона Кирхгофа:
(1.33)
При двух последовательно соединенных потребителях:
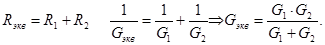(1.34)
|
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
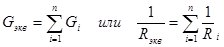(1.13)
Это следует из I закона Кирхгофа:
При двух параллельно соединенных потребителях:
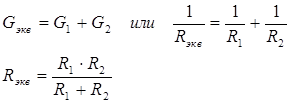(1.14)
Таким образом, для расчета цепей с последовательно включенными потребителями целесообразно их свойства выражать значениями сопротивлений, а для параллельно включенных – значениями проводимостей.
Определение эквивалентного сопротивления при смешанном соединении потребителей выполняется путем постепенного упрощения (сворачивания) исходной цепи.
Пример.
|
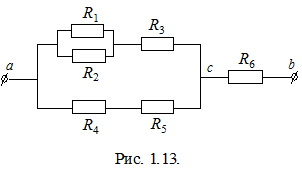
Параллельное соединение R1 и R2:
Последовательное соединение R12 и R3: 
Последовательное соединение R4 и R5: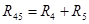 
Параллельное соединение R123 и R45: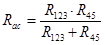 
Последовательное соединение Rас и R6: 
Таким образом, эквивалентное сопротивление
Более сложными являются взаимные преобразования потребителей, соединенных звездой или треугольником. К таким преобразованиям следует обращаться в тех случаях, когда в цепи, подлежащей упрощению, нельзя выделить параллельное или последовательное соединения потребителей.
В узлах a, b, c и треугольник, и звезда на рис. 1.14 соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены.
Выразим Uab треугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
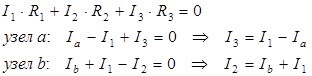
Заменим в первом уравнении токи I3 и I2 на соответствующие выражения:
По закону Ома напряжение Uab для соединения потребителей треугольником:
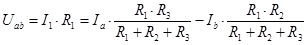(1.15)
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
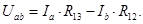(1.16)
Для эквивалентности данных цепей при произвольных значениях токов Ia и Ib необходимо равенство напряжений Uab для соединения потребителей треугольником и звездой. Это возможно только при одинаковых коэффициентах уравнений (1.15) и (1.16), т.е.
(1.17)
Аналогично можно получить выражения для определения 
:
(1.18)
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника.
Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений (1.17) и (1.18) через проводимости:
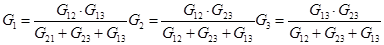(1.19)
или через сопротивления:
(1.20)
Следовательно, сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
