Задания к лабораторной работе №2
Работа в табличном процессоре Excel
Указания. Перед началом выполнения лабораторной работы изучите методические указания (см. файл: Word_ Excel _MathCAD_МетодУказания.pdf)
Лабораторная работа №4 состоит из трех заданий (1 – работа с мастером диаграмм; вычисление значений функции y(x) с использованием стандартных функций и построение графиков; 3 – построение трендов).
Задание 1. Работа с мастером диаграмм
1)Построить таблицу, рассчитать «Итого»; построить гистограмму (см. Рис. «Результат построения гистограммы» ниже). Данные для выполнения этого задания использовать свои.
2) Используя данные вашей таблицы, воспользуйтесь «Мастером диаграмм» (см. рис. «Окно Мастера диаграмм» ниже) и попытайтесь построить все имеющиеся «Стандартные Типы» графиков (диаграмм…). Проанализируйте результаты изображений.

Рис. Результат построения гистограммы

Рис. Окно Мастера диаграмм
Задание 2. Вычисление значений функции y(x) с использованием стандартных функций. Построение графиков.
Средствами Excel согласно вашему варианту рассчитайте значения функции и постройте график функции. Варианты заданий располагаются в приложении 1 (см ниже). (При необходимости некоторые стандартные функции и границы изменения переменной х можно заменить на более простые.) Задание оформить по образцу (см. ниже рис.).
Пример решения системы 2-х уравнений

а
Пример (вариант (I)) решения системы 3-х уравнений

б
Пример (вариант (II)) решения системы 3-х уравнений

в
Рис. Примеры решения системы уравнений средствами Excel
Задание 3. Построение трендовых моделей при помощи диаграмм
Повторите все указанные действия для построения трендовых моделей при помощи диаграмм (см. приложение 2). Затем измените данные второго столбца (по своему усмотрению) см.рис. 4 приложения 2. Результат построения графика и тренда изменится. Поясните эти изменения.
Замечание. Указания к построению трендов в Excel (версия 2010) см. в приложении 3
Приложение 1
Варианты к заданию 2
| 1) | 
|
| 2) | 
|
| 3) | 
|
| 4) | 
|
| 5) | 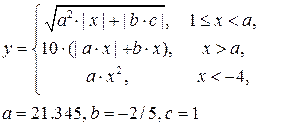
|
| 6) | 
|
| 7) | 
|
| 8) | 
|
| 9) | 
|
| 10) | 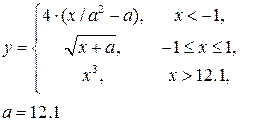
|
| 11) | 
|
| 12) | 
|
| 13) | 
|
| 14) | 
|
| 15) | 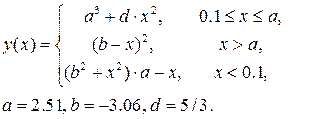
|
| 16) | 
|
| 17) | 
|
| 18) | 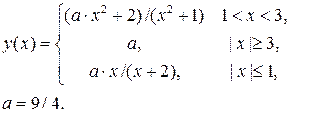
|
| 19) | 
|
| 20) | 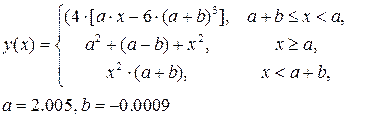
|
| 21) | 
|
| 22) | 
|
| 23) | 
|
| 24) | 
|
| 25) | 
|
Приложение 2
Построение трендовых моделей при помощи диаграмм
Многие экспериментальные данные можно интерпретировать как временные ряды - последовательность измерений, полученных в определенные моменты времени ti, где i - порядковый номер измерения на оси времени. Такие ряды характеризуются некоторой тенденцией развития процесса во времени и называются трендовыми. Используя трендовые модели, можно выдавать прогнозы на краткосрочный и среднесрочный периоды. Excel имеет средства для создания трендовых моделей встроенные в построитель диаграмм.
Одной из форм трендовых моделей при постоянном шаге по времени является линейная:
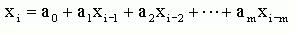
В качестве примера используем данные об авиаперевозках в США с 1949 по 1960 годы. Пусть требуется предсказать объем авиаперевозок на 1961 год. Знание этого объема позволяет планировать развитие авиационной промышленности и инфраструктуры, связанной с авиаперевозками. Исходные данные приведены в таблице.

Рис. 1.
Порядок расчетов следующий.
- Выделить диапазон B2:B13 и построить по этим данным диаграмму типа "График", щелкнув по значку "Мастер диаграмм" на панели инструментов.
- Выделить диаграмму и выполнить Диаграмма/Добавить линию тренда.

Рис. 2.
- В окне "Линия тренда" открыть вкладку "Параметры" и установить флажки "Показывать уравнение на диаграмме" и "Поместить на диаграмму величину достоверности аппроксимации".

Рис. 3.
4. На вкладке "Тип" выбрать тип диаграммы – линейная и нажать Ok. Результаты показаны на рисунке.

Рис. 4.
5. Вычислить по формуле y = 383,09x + 873,52. Следует учесть, что аргументом трендовой модели является порядковый номер, т.е. в нашем примере x =13. В результате получим прогноз на 1961 год: 5853,69 тысяч пассажиров.
Следует заметить, что мы, скорее всего, получили заниженный прогноз. Это видно из диаграммы и обусловлено выбором линейной модели прогноза. Возможно, что более точный прогноз был бы получен с помощью степенной или экспоненциальной линий тренда. Оценить качество прогноза можно только в конце 1961 года. В целом прогноз следует делать весьма осторожно – возможны большие ошибки. Именно поэтому чаще всего используются краткосрочные и среднесрочные прогнозы.
Коэффициент достоверности аппроксимации R2 показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R2 к 1, тем точнее модель описывает имеющиеся данные.
Приложение 3









