Задания к лабораторной работе №1
Работа с текстовым документом Word
Указания. Перед началом выполнения лабораторной работы изучите методические указания (см. файл: Word_Excel_MathCAD_МетодУказания.pdf)
· Задание 1. (по выбору (А) или (Б))
(A) - упрощенный вариант: Создать и отформатировать первую таблицу. (см. приложение 1).
(Б) - усложненный вариант: Создать и отформатировать первую таблицу. Затем скопировать созданную таблицу, для получения второй таблицы внести изменения в копию (см. приложение 1).
· Задание 2. Записать текст и математические соотношения, используя редактор формул (см. приложение 2).
· Задание 3. Создать векторный рисунок в Word по одному из образцов, представленных ниже в приложении 3 (выбор свободный, допускается создать свой векторный рисунок).
Средствами Word согласно вашему вариантувыполнить и оформить лабораторную работу:
· первая страница – титульный лист, который следует оформить по образцу (см. приложение 4);
· вторая страница должна содержать задание 1 (оформление таблиц) и результат его выполнения;
· третья страница должна содержать задание 2 (работа с редактором формул) и результат его выполнения.
· четвертая страница должна содержать задание 3.
Примечание. Для форматирования документа использовать специальные инструменты и меню, в том числе разрыв страницы. Страницы отчета пронумеровать (титульный лист не нумеровать).
Приложение 1.
Варианты 1–10 к заданию 1 «Создание и форматирование таблиц».
1)
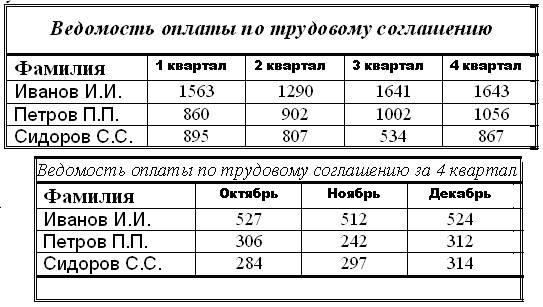
2)
3)
4)
5)
6)
7)
8)
9)
10)
Приложение 2.
Варианты 1–20 к заданию 2 «Работа с редактором формул».
1. Векторное произведение векторов a и b в координатной форме можно записать в виде определителя 3-го порядка:
.
.
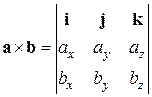3. Вычислить выражение
.
4. Производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя:
.
5. Элементы x и y вычисляются по формулам:
при 
Вычислить 
.
6. Вычислить выражение 
.
7. Найдите пределы указанных функций
а) 
, 
; б) 
; в) 
.
8. Значения членов числовой последовательности ai, bi вычисляются по формулам:
Не применяя массивов, вычислить 
при а1 = b1 = 1.
9. Дано действительное b<0. Последовательность 
образуется по следующим формулам:
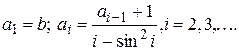
Не используя массивов, найти значение и номер первого неотрицательного члена последовательности.
10. Вычислить интеграл методом трапеций с точностью 0.0001
.
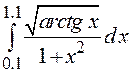11. Вычислить 
методом Симпсона с точностью 0.0001.
12. Вычислить 
методом Симпсона с точностью 0.0001.
13. Вычислить 
14. Вычислить 
15. Вычислить 
не используя функцию abs(x).
16. Вычислить значение определителя 
17. Найти решение системы линейных алгебраических уравнений методом Гаусса, если коэффициенты системы заданы матрицей
.
18. Найти решение системы линейных алгебраических уравнений
.
19. Найти решение системы линейных алгебраических уравнений
.
20. Найти решение системы линейных алгебраических уравнений
.
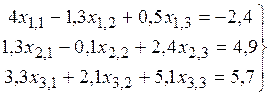Приложение 3.
Варианты 1–8 к заданию «Создание векторного рисунка в Word»
Приложение 4.
Форма титульного листа
для оформления отчета по лабораторной работе
Государственное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский Томский политехнический университет»
