Задание 1. Определение g с помощью математического маятника.
1. Рассчитать минимальную длину маятника 
, начиная с которой момент инерции можно рассчитывать по приближенной формуле 
, пренебрегая слагаемым 
.
Приборные погрешности в данной работе дают относительную погрешность результата 
(т. е. 1%), поэтому достаточно потребовать, чтобы
,
т. е. была на порядок меньше, чем 
(d - диаметр шарика).
Если 
, то погрешность пренебрежительно мала и маятник можно считать математическим.
2. Выбрать два значения 
и 
, так, чтобы разность 
была максимальна. Выбор согласовать с преподавателем.
3. Снять физический маятник с верхнего кронштейна. Установить верхний кронштейн таким образом, чтобы шарик математического маятника оказался в рабочей зоне фотодатчика.
4. Установить по шкале вертикальной стойки длину а1 математического маятника.
4. Нажать переключатель «Сеть», проверяя, все ли индикаторы измерителя показывают цифру нуль и горит ли лампочка датчика.
5. Привести маятник в движение, отклонив его приблизительно на 5о – 8о от положения равновесия.
6. С помощью секундомера измерить время 10 полных колебаний. Снять показания прибора.
7. Нажать кнопку «Сброс».
8. Пункты 5-7 повторить 3 раз.
9. Пункты 4-8 повторить для второй длины а2 математического маятника
Задание 2. Определить g с помощью оборотного маятника.
1. Повернуть верхний кронштейн на 1800.
2. Зафиксировать диски на стержне несимметрично таким образом, чтобы одна из них находилась вблизи конца стержня, а другая – вблизи его середины.
3. Призматические опоры маятника закрепить по обеим сторонам центра тяжести полученной системы таким образом, чтобы они были обращены друг другу лезвиями. Один из них поместить вблизи свободного конца стержня, а второй – на половине расстояния между дисками.
4. Проверить, соответствуют ли грани лезвий опор нарезкам на стержне.
5. Подвесить оборотный маятник на призматической опоре, находящейся вблизи конца стержня.
6. Привести маятник в движение, отклонив его на 5о – 8о от положения равновесия.
7. С помощью секундомера измерить время 10 колебаний. Повторить пункт 6-7 не менее 3 раз.
8. Снять маятник и закрепить его на второй призматической опоре. Если Т 1 > T, то опору переместить в направлении диска, находящегося в конце стержня. Если же Т 1 < T, то в направлении середины стержня. Расположение диска и первой опоры не менять.
17. Определить длину приведенного маятника, определив расстояние между ножками.
V. Таблицы измерений.
Задание 1.
1. Диаметр шарика d=; 
2.Первый опыт.
Число колебаний: n =10
Длина нити: 
; 
.
Время колебаний:
| № опыта | 
| 
|
| Среднее значение |
Расчет: 
; 
.
Период колебаний:
; 
; 
.
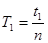3. Второй опыт оформить аналогично, записав результаты измерений в виде:
; 
.
Задание 2.
1. Время 10 колебаний.
| № опыта | 
| 
|
| Среднее значение |
2. Период колебаний:
; 
;
3. Приведенная длина (расчет на основе Т2): 
4.Период после оборота маятника: 
Точность выполнения равенства 
: 
5. Приведённая длина (расстояние между ножами).
; 
; 
VI. Обработка результата.
Задание 1.
1.По формуле (2) рассчитать g.
2.Определить погрешность 
по формуле:
.
3. Записать окончательный результат измерений:
Задание 2.
1. Используя формулу (3), определить ускорение свободного падения: 
.
2. Определить погрешность по формуле:
.
3. Записать окончательный результат измерений:
4. Сравнить полученные значения ускорения свободного падения с истинным: 
. Погрешность определения g не должна превышать 1%. Сделать вывод о качестве проведённых экспериментов.
Контрольные вопросы.
1. Что называется математическим маятником?
2. Что называется физическим маятником?
3. Что называется приведенной длиной физического маятника?
4. Сформулируйте теорему Штейнера.
5. Что есть «центр качания»?
6. Какой маятник называется оборотным?
7. Выведите формулы для периодов колебаний математического и физического маятников.
8. Как направлены вектор момента силы тяжести 
и вектор углового ускорения 
, когда маятник движется к положению равновесия? От положения равновесия?
