Определяемые в анализе рядов динамики показатели изменения уровней, тренда имеют широкое применение при прогнозировании, т.е. при получении статистической оценки возможной меры развития социально-экономических явлений на будущее. Важное значение при этом имеют статистические методы экстраполяции и прогнозирования.
Под экстраполяцией понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее.
Более широкое понятие представляет собой прогнозирование, основой которого является предположение, что закономерность, действующая внутри анализируемого ряда динамики, выступающего в качестве базы прогнозирования, сохраняется и в дальнейшем. Точность прогноза зависит от того, насколько обоснованными окажутся предположения о сохранении на будущее действий тех факторов, которые сформировали в базисном ряду динамики его основные компоненты.
Важное значение при экстраполяции имеет продолжительность ряда динамики и сроков прогнозирования. При экстраполяции динамики социально-экономических явлений следует брать те субпериоды базисного ряда динамики, которые составляют определенный этап в развитии изучаемого явления. Установление сроков прогнозирования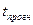 
зависит от задачи исследования. Следует иметь в виду, что чем короче сроки упреждения прогноза, тем надежнее результаты.
Применение методов экстраполяции зависит от характера изменений в базисном ряду динамики и предопределяется задачей исследования.
1. Линейные прогнозы. При экстраполяции уровней развития изучаемого явления на базе ряда динамики с постоянными абсолютными приростами (
) применяется формула:
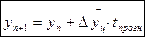(5.1)
где 
- экстраполируемый уровень,
- конечный уровень базисного ряда динамики
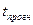- срок прогноза.
Для построения линейных прогнозов в MS Excel используется статистическая функция ТЕНДЕНЦИЯ, которая возвращает значения в соответствии с линейной аппроксимацией по методу наименьших квадратов.
2. Нелинейные прогнозы. При экстраполяции уровня развития изучаемого явления на базе ряда динамики со стабильными цепными темпами роста (
) применяется формула:
(5.2)
Для построения нелинейных прогнозов в MS Excel используется статистическая функция РОСТ, которая рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных.
При прогнозировании тенденции изучаемого явления на основе аналитического выравнивания для экстраполяции тренда применяются адекватные трендовые модели.
При составлении прогнозов используют интервальную оценку. Величина доверительного интервала определяется выражением:
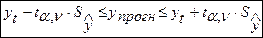(5.3)
где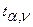 
- значение t-критерия Стьюдента для заданной доверительной вероятности 
и числа степеней свободы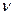 
;
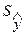- среднее квадратическое отклонение от тренда, определяемое по формуле:
(5.4)
где 
и 
- соответственно эмпирическое и расчетное значения уровней ряда;
n – число уровней ряда;
m – количество параметров в уравнении ряда (для прямолинейной функции 
m = 2).
n – m = v - число степеней свободы.
Задание №5. Линейные прогнозы рядов динамики.
Условие задачи. По данным о численности населения г. Минска на 1991-2001 г.г необходимо спрогнозировать численность населения на 2002 год.
Ход выполнения
Скопируйте данные о численности населения г. Минска с листа Задание 5 на новый лист и присвойте ему имя Линейный прогноз.
Добавьте фрагмент книги согласно рис. 7.11.
Рис.7.11.
1-й способ (по формуле). Определите в ячейке С16 по формуле (5.1) возможную численность населения г. Минска в 2002 г., учитывая, что рассчитанный средний абсолютный прирост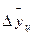 
= 5,5 тыс.чел.
2-й способ (на основе трендовой модели). Используя уравнение полученной трендовой модели (см. данные листа Трендовая модель), сделайте прогноз населения г. Минска на 2002 год в ячейке С17. Для этого найдите значение теоретического уровня 
при t =6.
3-й способ (с использованием функции ТЕНДЕНЦИЯ). Сделайте прогноз населения г. Минска в 2002 г. в ячейке С18, используя статистическую функцию ТЕНДЕНЦИЯ. Для этого:
Установите курсор в ячейку С18.
Вызовите функцию ТЕНДЕНЦИЯ (категория Статистические).
В диалоговом окне установите параметры согласно рис. 7.12.
Рис.7.12. Окно функции ТЕНДЕНЦИЯ
где Известные_значения_у – это массив известных значений уровней ряда динамики, которые описываются линейной трендовой моделью .
Известные_значения_х – известные периоды времени (необязательный параметр).
Новые_значения_х – период времени, на который рассчитывается прогноз.
Сравните полученные результаты с рис. 7.13.
Рис.7.13. Прогноз на 2002 год
4-й способ (графический). На листе Трендовая модель для линии тренда на вкладке Параметры установите опцию «Прогноз» на один период вперед.
Проанализируйте полученные результаты.
Найдите доверительный интервал, в пределах которого находится 
. Для этого:
На листе Трендовая модель рассчитайте 
и 
в ячейках G3:G13 и ячейках Н3:Н13 соответственно.
В ячейке Н14 найдите сумму квадратов отклонений эмпирических и расчетных значений ряда динамики 
.
В ячейке Н16 по формуле (5.4) рассчитайте среднее квадратическое отклонение 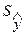, учитывая, что число уровней ряда динамики n=11, а число параметров прямолинейного уравнения m =2.
Учитывая, что для заданных доверительной вероятности и числу степеней свободы 
значение t-критерия Стьюдента 
, по формуле (5.3) найдите доверительный интервал, в пределах которого лежит прогнозируемое значение .
Определите, входит ли прогнозируемое значение, рассчитанное по формуле (5.1), в полученный доверительный интервал.
Задание №6. Нелинейные прогнозы рядов динамики
Для исследования возможностей прогнозирования в случае нелинейной зависимости на новом листе Нелинейный прогноз введите данные столбцов А (Неделя) и В (Заказы) согласно рис. 7.14.
Рис.7.14. Данные для нелинейного прогноза
Для построения прогноза на период 11-13, воспользуйтесь статистической функцией РОСТ. Для этого:
Выделите диапазон ячеек С2:С14.
Вызовите функцию РОСТ (категория Статистические).
В диалоговом окне установите параметры согласно рис. 7.15.
Нажмите комбинацию клавиш SHIFT+CTRL+ENTER.
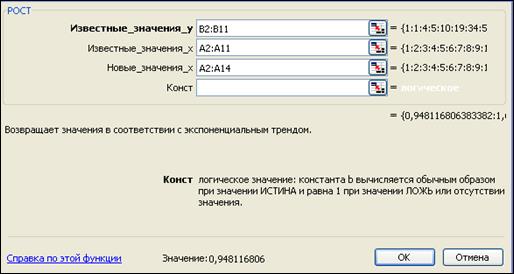
Рис. 7.15
где Известные_значения_у – это массив известных значений уровней ряда динамики, которые описываются экспоненциальной трендовой моделью со стабильными темпами роста (
).
Известные_значения_х – известные периоды времени (необязательный параметр).
Новые_значения_х – периоды времени, на которые делается прогноз.
Постройте график для изучаемого ряда динамики. На график добавьте линию тренда (тип тренда – экспоненциальный). На вкладке «Параметры» установите флажок «Показать уравнение на диаграмме», укажите «Прогноз» на три периода вперед.
Добавьте на график ряд на основе функции РОСТ.
Сравните прогноз, полученный графическим способом и рассчитанный с помощью функции РОСТ, и сделайте выводы.
Контрольные вопросы
1. Что такое ряды динамики?
2. Укажите основные элементы рядов динамики.
3. Как рассчитать показатели изменения рядов динамики цепным методом?
4. Что такое абсолютный прирост?
5. Чем темп роста отличается темпов прироста?
6. Как вычислить средний абсолютный прирост, средние темпы роста и среднего прироста.
7. Как рассчитать показатели изменения рядов динамики базисным методом?
8. Опишите технологию выявления основной тенденции развития рядов динамики методом укрупнения интервалов.
9. Опишите технологию выявления основной тенденции развития рядов динамики методом скользящих средних
10. Опишите технологию анализа основной тенденции развития ряда динамики методом аналитического выравнивания.
11. Что такое экстраполяция?
12. Чем линейный прогноз отличается от нелинейных?
Лабораторная работа №8
