| Коэффициент корреляции rxy | Теснота связи |
| + 0,91-1,0 | Очень сильная |
| + 0,81-0,9 | Весьма сильная |
| + 0,65-0,8 | Сильная |
| + 0,45-0,64 | Умеренная |
| + 0,25-0,44 | Слабая |
| До + 0,25 | Очень слабая |
| «+» - прямая зависимость «-» - обратная зависимость |
T-статистика Стьюдента
Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле
 .
.
Полученную величину tрасч сравнивают с табличным значением t-критерия Стьюдента с n-2 степенями свободы. Если tрасч > tтабл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y d в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если tрасч < tтабл, то величины X и Y независимы.
Регрессионный анализ
Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели.
Уравнение линейной регрессии имеет вид:
Y=a1X1 + a2X2 + …+ akXk, где а1, а2… аk – параметры, подлежащие определению методом наименьших квадратов (МНК). В среде MS Excel для этого используется встроенная функция ЛИНЕЙН и инструмент Регрессия из Пакета анализа.
Задание 1. Исследование связей между двумя исследуемыми признаками.
Условие задачи. По 20 туристическим фирмам были установлены затраты на рекламную кампанию и количество туристов, воспользовавшихся после ее проведения услугами каждой фирмы. Определить коэффициент корреляции между исследуемыми признаками.
Ход выполнения:
Откройте новую книгу MS Excel и создайте таблицу согласно рис. 6.1:

Рис.6.1.
Рассчитайте в ячейке С23 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические.
Синтаксис функции:
КОРРЕЛ (массив1; массив 2):
где массив1 – ссылка на диапазон ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек второй выборки (Y).
В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B21;C2:C21).
Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов.

Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н0: rxy=0 и альтернативная Н1: rxy≠0. Для проверки гипотезы Н0 рассчитайте t-статистику Стьюдента по формуле, указанной выше в ячейке С24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 и формула будет следующей: =C23*КОРЕНЬ(20-2)/КОРЕНЬ(1-(C23*C23)).
Сравните полученное значение с критическим значением tν,α распределения Стьюдента. (При ν =18 и доверительной вероятности α = 0,05, tν,α, табл = 1,734). Сделайте вывод о наличии связи между исследуемыми величинами.

Задание 2. Построение регрессионной модели.
1-й способ. Функция ЛИНЕЙН.
В первом способе для получения коэффициентов а и b линейного уравнения регрессии Y=а*X+b, описывающего зависимость количества привлеченных туристов от затрат на рекламу воспользуемся статистической функцией ЛИНЕЙН. Для этого выделите две ячейки C26:D26 и выполните вставку функции ЛИНЕЙН с аргументами согласно рис.6.2.
Здесь Известные_значения_y – диапазон значений Количество туристов, Известные_значения_x – диапазон значений Затраты на рекламу. Нажмите комбинацию клавиш SHIFT+CTRL+ENTER.
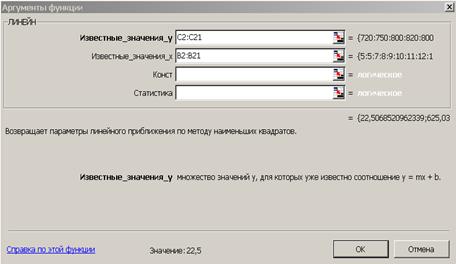
Рис. 6.2. Аргументы функции ЛИНЕЙН
В ячейку D27 введите уравнение Y= a*X+b (вместо a и b подставьте полученные коэффициенты линейной регрессии).







