I курс, 1 семестр.
Кременчук
Розповсюдження і тиражування без офіційного дозволу ІЕНТ і авторів заборонено.
Методичні рекомендації до самостійного вивчення вищої математики на економічному факультеті
(розділ ІV. Вступ до математичного аналізу. I курс, 1семестр).
Укладач: Тристан Віктор Миколайович, старший викладач.
Рецензент: Семенов В.О, кандидат фізико-математичних наук, професор.
Комп’ютерний набір: Тристан А.В.
Відповідальний за випуск: професор Семенов В.О.
Методичні рекомендації розглянуті та рекомендовані до видання на засіданні кафедри прикладної математики та математичного моделювання від 30 серпня 2003р., протокол № 1
Схвалено методичною радою ІЕНТ “_____”_______________р.,
протокол №______.
Затверджено Вченою радою ІЕНТ “_____”_______________р.,
протокол №______.
Наклад 50 примірників
Передмова
Методичні рекомендації адресовані студентам економічного факультету, які навчаються за спеціальностями „Облік та аудит” і „Маркетинг” стаціонарно та заочно. Вони містять необхідний теоретичний матеріал і розв’язання типових задач ІV розділу курсу вищої математики для економістів „Вступ до математичного аналізу”, що вивчається в першому семестрі.
Мета методичних рекомендацій полягає у тому, щоб допомогти студентам засвоїти цей розділ курсу вищої математики та набути навичок самостійної роботи при розв’язуванні задач.
Методичні рекомендації містять завдання контрольної роботи в 34 варіантах.
З метою самоконтролю за вивченням курсу до методичних рекомендацій внесено питання для підготовки до екзамену.
Методичні вказівки містять список рекомендованої літератури.
І. Основні питання, що вивчаються в розділі.
І. Функції. Класифікація функцій.
ІІ. Границя функції однієї змінної.
1. Означення границі функції у точці.
2. Нескінченно малі величини.
3. Основні теореми про границі. Ознаки існування границі.
4. Обчислення границі функції в точці.
4.1. Границі многочлена та дробово-раціональної функції.
4.2. Границі тригонометричних функцій. Перша важлива границя.
4.3. Друга важлива границя.
4.4. Границі показникових та логарифмічних функції.
4.5. Границі ірраціональних функцій.
4.6. Границя функції на нескінченності.
ІІІ. Неперервність функцій.
- Означення неперервності.
- Точки розриву. Класифікація.
- Властивості неперервних функцій.Арифметичні операції над неперервними функціями.
- Властивості функцій, неперервних на відрізку.
- Дослідження функцій на неперервність.
ІІ. Основні теоретичні відомості. Приклади розв’язання задач.
І. Функції. Класифікація функцій.
Класифікація елементарних функцій за характером аналітичних дій, які вказані у формулі 
.
Многочлени. Так називаються функції, які одержують з х тільки першими трьома арифметичними діями: додаванням, відніманням та множенням. Загальний вигляд многочлена: 
.
Раціональні функції. 
, де 
і 
– многочлени. Одержують з х за допомогою чотирьох арифметичних дій: додавання, віднімання, множення та ділення.
Явні алгебраїчні функції. До чотирьох арифметичних дій додають дію добування радикалів будь-яких степенів. Функція називається явною, коли відомі всі дії, які треба виконати над аргументом х, щоб одержати у (права частина не містить незалежної змінної х).
Якщо для визначення функції у аргументу х задане тільки рівняння 
, що не розв’язане відносно у, тоді функція у називається неявною функцією аргументу х.
Трансцендентні функції:
- степенева: 
, де 
– ірраціональне число;
- показникова: 
;
- логарифмічна: 
;
- тригонометричні функції у= sin x, y= cos x, y= tg x,
y= ctg x;
- обернені тригонометричні функції: y= arcsin x,
y= arcсos x, y= arctg x, y= arcctg x;
ІІ. Границя функції однієї змінної.
1. Означення границі функції у точці
Означення 1. Число Аназивається границею функції 
при 
або в точці х0, якщо для будь-якого числа 
існує таке число 
, що для всіх 
, 
і таких, що 
, справджується нерівність 
. Символічно це записують так: 
.
Зауваження 1. Словосполучення „ і таких, що ” можна записати скорочено у вигляді нерівності 
.
Зауваження 2. Умова накладена для того, щоб охопити випадки, коли у точці 
функція не визначена, а якщо , то вона має границю – число А.
Геометрична інтерпретація границі функції у точці має такий вигляд:
Теорема 1
Границя лінійної функції у точці дорівнює значенню функції у цій точці, тобто 
.
Доведення
Щоб довести дану рівність, треба показати, що для будь-якого додатного числа існує додатне число 
, таке, що з нерівностей випливає нерівність 
(*).
Знайдемо число . Для цього у лівій частині нерівності виконаємо тотожні перетворення 
, 
, 
. Звідси 
.
Отже, якщо взяти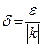 
, то для всіх х, які задовольняють нерівність 
, справджується нерівність (*).
Приклад 1
Довести, що 
Розв’язання.
Задамо додатне число і знайдемо число 
, таке, щоб для всіх 
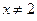і таких, що 
справджувалась нерівність 
.(1) Щоб знайти , слід розв’язати останню нерівність відносно 
. Для цього застосуємо прийом підсилення нерівності. Виконаємо тотожні перетворення у лівій частині нерівності (1).
Дістанемо: 
, або 
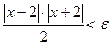.(2).
Замінимо в нерівності (2) множник 
на число 5, яке він не перевищує, бо < 1, коли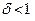 
. При цьому одержимо 
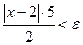(3).
Якщо справджується нерівність (3), то справджується рівносильна їй нерівність (2). З нерівності (3) дістанемо 
. Таким чином, за можна взяти менше з двох чисел 1 і 
. Отже, якщо 
. Нерівність доведено.
2. Нескінченно малі величини
Означення 2. Функція 
називається нескінченно малою при 
, якщо її границя дорівнює нулю:
.
Теорема 2
Якщо функція має при границю, що дорівнює А, то її можна подати так: = А + .
Властивості нескінченно малих.
Властивість 1
Сума будь-якого скінченого числа нескінченно малих величин є нескінченно малою величиною.
Властивість 2
Добуток нескінченно малої величини на обмежену функцію є нескінченно малою величиною.
Властивість 3
Частка від ділення нескінченно малого на функцію, границя якої відмінна від нуля, є нескінченно малою величиною.
3. Основні теореми про границі. Ознаки існування границі
Теорема 3
Функція не може мати більше однієї границі.
Нехай відомо, що 
, 
.
Теорема 4
Границя алгебраїчної суми скінченого числа функцій дорівнює сумі границь цих функцій, тобто 
.
Теорема 5
Границя добутку скінченого числа функцій дорівнює добутку границь цих функцій, тобто 
.
Наслідок. Сталий множник можна виносити за знак границі.
Теорема 6.
Границя частки двох функцій дорівнює частці границь (за умови, що границя дільника не дорівнює нулю).
, 
.
Теорема 6.
Про границю суперпозиції двох функцій.
Якщо 
, 
, тоді 
.
Теорема 7.
Якщо в околі деякої точки 
: 
, тоді 
Теорема 8.
Якщо в околі деякої точки : 
, 
, тоді 
.
4. Обчислення границі функції в точці.
Доводити, що число є границею функції у точці з одного боку складно, з іншого не завжди можливо наперед знати границю. Тому виникає проблема обчислення границь конкретних елементарних функцій у заданих точках. Для розв’язання цієї задачі використовують основні формули, які доводяться на основі теорем про границі.
1. 
(4.1)
2. 
(4.2)
3. 
(4.3)
4. 
(4.4)
5. 
(4.5)
Формули (4.1) – (4.5) мають місце за умови, коли границі 
існують і не дорівнюють нескінченності.
4.1. Границі многочлена та дробово-раціональної функції у точці.
Теорема 9
Границя многочлена у точці дорівнює значенню многочлена у цій точці, тобто 
, де 
Для доведення використовують основні формули та теорему 1 (
).
Теорема 10
Границя раціональної функції 
, де 
– многочлени, у точці а дорівнює значенню цієї функції у точці, тобто 
, якщо 
.
Доведення проводимо, використовуючи основні формули та теорему 9.
Приклад 2
Знайти границю: 
Розв’язання.
Використаємо теорему 10 і одержимо: 
Приклад 3
Знайти границю: 
.
Розв’язання.
При знаходженні цієї границі ми не можемо використати теорему 10, бо границя знаменника дорівнює нулю. Підстановка числа 
під знак границі приводить до невизначеності типу 
. Для обчислення границі розкладаємо чисельник та знаменник на множники і скорочуємо на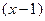 
:
= = 
.
Зауваження. Якщо х=а – корінь многочлена , тобто 
, то за наслідком теореми Безу ділиться без остачі на 
, тому його можна розкласти на множники: 
, де 
– многочлен.
Приклад 4
Знайти границю: 
.
Розв’язання.
= 
.
4.2. Границі тригонометричних функцій. Перша важлива границя.
Теорема 11
.
Теорема 12
.
Теорема 13
.
Цю границю називають першою важливою границею.
Приклади 5 – 8
Знайти границі.
5. 
6. 
7. 
8. 
Теорема 14
.
Теорема 15
.
Приклади 9 – 10
Знайти границі.
9. 
.
10. 
Означення 3. Дві нескінченно малі функції називаються еквівалентними, якщо 
Позначаються 
.
Розглянуті приклади дозволяють записати такі еквівалентні нескінченно малі функції:
.
При знаходженні границь доцільно нескінченно малі функції заміняти еквівалентними.
Приклад 11
Знайти границю: 
;
Розв’язання.
= 
= 
= = 
= 
Друга важлива границя.
Означення 4. Границя змінної величини 
при 
називається числом е (
– ірраціональне число).
Теорема 15
Друга важлива границя. 
, або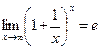 
.
Друга важлива границя використовується при розкритті невизначеності типу 
.
Приклад 12
Знайти границю: 
Розв’язання.
= = 
= 
= 
= 
= 
.
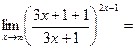
Для розкриття невизначеності типу використовують простий прийом: 
= 
.
Приклад 13
Знайти границю: 
Розв’язання.
= = 
= 
= 
4.4. Границі показникових та логарифмічних функції.
Теорема 16
.
Теорема 17
, 
.
Приклад14
Знайти границю: 
Розв’язання.
= 
= 
= 
= = 
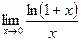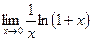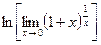Приклад 15
Знайти границю: 
Розв’язання.
= 
.
Зауваження. Приклади 14 і 15 дають ще дві еквівалентні нескінченно малі, які доцільно використовувати при обчисленні границь. 
.
4.5. Границі ірраціональних функцій.
Теорема 18
, 
.
Приклад 16
Знайти границю: 
.
Розв’язання. = 
= 
= = 
= 
4.6. Границя функції на нескінченності.
Означення 14. Число А називається границею функції 
, коли 
, якщо для будь-якого додатного числа 
існує таке додатне число М, що із нерівності 
випливає нерівність 
.
Аналогічно означають границю, коли 
.
Запишемо поведінку відомих елементарних функцій на нескінченності.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. Границі тригонометричних функцій 
на нескінченності не існують.
Теорема 19
= 
Приклад 17
Знайти границю: 
.
Розв’язання.
= 
(використано теорему 19)
Приклад 18
Знайти границю: 
.
Розв’язання.
= 
(використано теорему 19)
Приклад 19
Знайти границю: 
Розв’язання.
= 
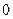(використано теорему 19)
ІІІ. Неперервність функцій.
1. Означення неперервності.
Означення 5
Функція 
називається неперервною в точці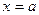 
, якщо:
1) функція визначена в точці 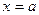і деякому її околі;
2) ця границя дорівнює значенню функції в точці 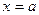, тобто 
= 
Зауваження 1. З умови неперервності випливає, що = 
.
Це дає правило граничного переходу під знаком неперервної функції.
Зауваження 2. Умова неперервності може також бути представлена в вигляді: 
Ця умова означає, що для неперервної в точці 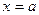функції, границя функції справа в точці 
дорівнює границі функції зліва в точці і дорівнює значенню функції в цій точці.
2. Точки розриву. Класифікація.
Означення 6. Точка , в якій порушена хоча б одна з умов неперервності, називається точкою розриву функції .
Точки розриву класифікують таким чином:
1. Якщо існують скінченні границі 
і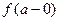 
, причому не всі три числа , 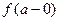і рівні між собою, то точка називається точкою розриву першого роду.
До точок розриву першого роду відносяться точки усувного розриву та точки розриву типу „стрибок”.
1.1. Якщо = 
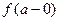
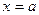, то точка називається точкою усувного розриву.
1.2. Якщо 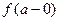, то точка 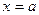називається точкою „стрибка”, а величина: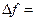 
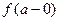- стрибком функції в точці .
2. Точка називається точкою розриву другого роду функції , якщо хоча б одна з границь , 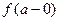не існує або дорівнює нескінченності.
3. Властивості неперервних функцій. Арифметичні операції над неперервними функціями .
Теорема 21
Якщо функції та 
неперервні в точці 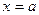, тоді в цій точці неперервні функції:
Теорема 22
Про неперервність складної функції.
Якщо функція 
неперервна в точці , а функція 
неперервна в точці 
, то складна функція 
неперервна в точці .
Теорема 23
Про н еперервність оберненої функції.
Якщо функція визначена, зростаюча (спадна) і неперервна на відрізку 
, де 
, 
. Тоді ця функція має на відрізку обернену функцію 
або 
, яка є зростаючою (спадною) і неперервною.
Теорема 24
Про неперервність елементарних функцій.
Елементарні функції неперервні в усіх точках, в яких вони визначені.
4. Властивості функцій, неперервних на відрізку.
Функція , неперервна на відрізку , має такі властивості:
1. обмежена на відрізку ;
2. досягає на відрізку свого найбільшого та найменшого значення;
3. набуває всіх проміжних значень між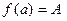 
і 
, 
, тобто для будь-якого числа 
, що лежить між числами 
та 
, знайдеться така точка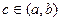 
, що 
;
4. за умови, що 
, існує хоча б одна точка 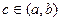така, що 
5. Дослідження функцій на неперервність.
При знаходженні точок розриву потрібно враховуватитакі факти:
1. Елементарна функція може мати розрив тільки в окремих точках, але не може бути розривною в усіх точках будь-якого інтервалу.
2. Елементарна функція може мати розрив тільки в тій точці, де вона не визначена, за умови, що вона визначена хоча б з однієї сторони від цієї точки.
3. Якщо функцію задано декількома різними аналітичними виразами (формулами) для різних інтервалів зміни аргументу, то вона може мати розриви в тих точках, де змінюється її аналітичний вираз.
Приклад 20
Дослідити на неперервність функцію 
, визначити точки розриву і встановити їх характер.
Розв’язання.
Функція визначена для всіх х, крім х = 3, і неперервною на інтервалах 
.
Обчислимо 
і 
: = 
= 
Маємо, що = 
, бо при х = 3 функція невизначена. У точці х = 3 маємо розрив першого роду – усувний.
Приклад 21
Дослідити на неперервність функцію: 
, визначити точки розриву і встановити їх характер.
Розв’язання.
Маємо показникові функцію, яка неперервна в кожній точці її області визначення. У точці х =2 функція не визначена.
Отже, функція неперервна на інтервалах 
. Обчислимо 
і 
:
= 
= 
У точці х = 2 функція має розрив другого роду.
Приклад 22
Дослідити на неперервність функцію: 
, визначити точки розриву і встановити їх характер.
Розв’язання.
Функція визначена в усіх точках, крім 
(це корені рівняння 
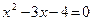). Отже, функція неперервна на інтервалах 
Розрив можливий тільки в точках .
Дослідимо характер точок розриву. Врахуємо, що = 
. 
= 
= 
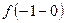. Маємо = 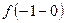, отже, точка х = -1 – точка усувного розриву.
= 
= 
Точка х =4 – точка розриву другого роду.
Приклад 23
Дослідити на неперервність функцію: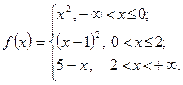 
, визначити точки розриву і встановити їх характер. Побудувати її графік.
Розв’язання.
Функція визначена і неперервна на інтервалах 
, де вона задана неперервними елементарними функціями. Розрив можливий тільки в точках 
.
Визначимо характер точок розриву. 
.
У точці х = 0 функція має розрив роду, типу „стрибок”.
.Отже, , тому у точці 
має розрив першого роду, типу „стрибок”.
Графік заданої функції має вигляд:
ІV. Завдання для контрольної роботи.
Завдання 1
Знайти границі заданих функцій.
Варіанти завдань:
1 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
2 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
3 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
4 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
5 а) 
| б) 
| |
в) 
| г) 
| |
| д)
| ||
6 а) 
| б) 
| |
в)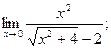 
| г) 
| |
д)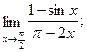 
| ||
7 а) 
| б)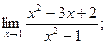 
| |
в)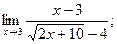 
| г)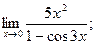 
| |
д) 
| ||
8 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
9 а) 
| б) 
| |
в) 
| г)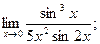 
| |
д) 
| ||
10 а) 
| б) 
| |
в) 
| г) 
| |
д)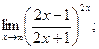 
| ||
11 а)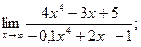 
| б)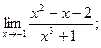 
| |
в) 
| г) 
| |
д) 
| ||
12 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
13 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
14 а) 
| б)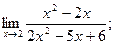 
| |
в) 
| г) 
| |
д) 
| ||
15 а) 
| б) 
| |
в) 
| г)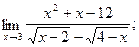 
| |
д) 
| ||
16 а) 
| б) 
| |
в) 
| г) 
| |
д) 
|
17 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
18 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
19 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
20 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
21 а) 
| б) 
| |
в) 
| г) 
| |
д) 
| ||
22 а) 
| б) 
| |
в) 
| г)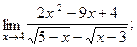 
| |
| д) | ||
|
|
|
|
|
|
Дата добавления: 2015-10-19; Мы поможем в написании ваших работ!; просмотров: 1814 | Нарушение авторских прав
Лучшие изречения:
| 2151 - 