Распределение напряженности электрического поля и

потенциала в ОПЗ. Длина ОПЗ

 

Рассмотрим случай плоского, резкого, несимметричного p-n-перехода. Не будем учитывать вклад электронов и дырок в электрическое поле в ОПЗ. (рис..).

В начале рассмотрим качественно картину распределения зарядов, напряжённости электрического поля и потенциала в ОПЗ, например, для случая N_a > N_d (рис…а), без учёта наличия подвижных носителей заряда в ОПЗ.

Плоский переход позволяет рассмотреть одномерный случай. По механизму образования двойного слоя количество положительных и отрицательных ионов в ОПЗ одинаково. Поскольку N_a > N_d, плотность отрицательных зарядов в p-области будет больше, чем положительных в n-области. Поэтому ширина ОПЗ в p-области d_p будет меньше чем ширина ОПЗ в n-области d_n (рис…б). На рис…в изображено распределение плотности зарядов ионов по координате x. Площади под кривыми распределения плотности зарядов должны быть равными, так как пропорциональны величинам одинаковых зарядов разного знака. Коэффициент пропорциональности - площадь p-n-перехода.

Поскольку переход плоский, то линии напряжённости электрического поля, идущие от слоёв положительных и отрицательных ионов, идут параллельно. Напряжённость поля прямо пропорциональна количеству зарядов. Поэтому вне ОПЗ они полностью компенсируют друг друга и напряжённость поля вне ОПЗ равна нулю. Если поместить пробный положительный заряд в середину слоя отрицательных ионов (координата -d_p/2), то силы действующие на него со стороны отрицательных зарядов будут равны и противоположно направлены. На него будут действовать только отталкивающие силы всех положительных зарядов. Поэтому напряжённость поля будет отрицательной (сила направлена против оси x). На металлургической границе (координата 0), на пробный заряд действуют силы притяжения от всех отрицательных зарядов и также направленные силы отталкивания от всех положительных зарядов. Поскольку напряжённость в нашем случае пропорциональна величинам зарядов, то она станет вдвое большей, чем в предыдущей точке. Если поместить пробный заряд в середину слоя положительных зарядов (координата d_n/2), то силы, действующие со стороны положительных зарядов, будут равны, противоположно направлены и скомпенсируют друг друга. На заряд будут действовать только силы притяжения со стороны отрицательных зарядов. Поэтому напряжённость поля, оставаясь отрицательной, уменьшится вдвое. Аналогичные рассуждения можно провести для любой точки ОПЗ и убедиться, в линейном распределении напряжённости электрического поля (рис…г).

Работа по перемещению пробного заряда через ОПЗ, делённая на величину пробного заряда, даст значение разности потенциалов. Интегрирование линейной функции распределения напряжённости даст параболический закон распределения потенциала в ОПЗ с перегибом в области металлургической границы (рис..д). Разность потенциалов при отсутствии внешнего источника напряжения будет равна контактной разности потенциалов j_к. Если приложить к электродам p-n-перехода внешнее напряжение U, то оно в зависимости от полярности может увеличить или уменьшить разность потенциалов на p-n-переходе. Если не учитывать падение внешнего напряжения на электронейтральных областях структуры, то разность потенциалов на p-n-переходе определяется алгебраической суммой контактной разности потенциалов и внешнего напряжения j_k - U. Если внешнее напряжение уменьшает потенциальный барьер, то оно называется прямым. Прямое напряжение U в выражении j_k - U берется со знаком "+". Если напряжение увеличивает потенциальный барьер, то это обратное напряжение, и берётся оно со знаком "-". ***********

Выведем аналитическое выражение для резко несимметричного перехода, воспользовавшись уравнением Пуассона:

,

где r(x) – плотность зарядов, e - диэлектрическая проницаемость полупроводника, e₀ – диэлектрическая постоянная вакуума. Для резкого перехода N(x) = N_a в p-области и N(x) = N_d в n-области. Тогда

при ,

при ,

при

Oбозначим через d ширину области ОПЗ:

.

Из равенства положительного и отрицательного заряда в ОПЗ следует

 

.

 

Будем учитывать, что диэлектрическая проницаемость одинакова в p- и n- областях. Уравнение Пуассона может быть преобразовано к виду

.

Проинтегрируем обе части, устанавливая переменным верхний предел интегрирования

.

Проинтегрируем еще раз

Интегрирование производных от -d_p до х учитывает действие силы алгебраической суммы зарядов, находящегося в этом промежутке и равного ему заряда в n-области на пробный заряд. (У плоского слоя заряда одного знака линии напряжённости идут перпендикулярно от плоскости в обе стороны и представляют собой параллельные прямые. Поэтому сила, действующая от 2-х слоёв зарядов, может быть заменена суммой сил, действующих от одного слоя. Для её определения берётся интеграл по поверхности, охватывающей заряд. Равнодействующая силы, действующей на пробный заряд от заряда, расположенного в интервале от x до 0 в p-области и равного ему заряда, расположенного в интервале от нуля до координаты, ограничивающей этот заряд в n-области, равна нулю.)

Определим производную потенциала электрического поля в p-области

и распределение потенциала

Проделаем эти расчеты для области n:

Рассчитаем длину ОПЗ:

 

 

 

При увеличении прямого напряжения ОПЗ уменьшается. При увеличении обратного напряжения ОПЗ растет. В резко несимметричном переходе (например N_a>N_d) ОПЗ располагается в основном в наименее легированной n-области.

 

 

Пусть N_a>>N_d, тогда N_d в уравнении (1) можно пренебречь. (14)

 

 

 

 

 

Существуют плавные переходы с линейным распределением примеси и постоянным градиентом концентрации a

.

Для таких переходов ширина ОПЗ вычисляется следующим образом

.

Для иных функций распределения концентрации примесей в p-n-переходе отсутствуют аналитические формулы, и ширина ОПЗ определяется численным интегрированием уравнения Пуассона.

 

Полупроводниковые диоды

 

Полупроводниковый диод – это полупроводниковый прибор с одним выпрямляющим электрическим переходом и двумя выводами, в котором используется то или иное свойство выпрямляющего электрического перехода.

В качестве выпрямляющего перехода в диодах может быть p-n-переход, гетеропереход или выпрямляющий переход металл-полупроводник (переход Шотки). Наряду с выпрямляющим переходом в диодах на основе p-n-перехода (гомоперехода или гетероперехода) имеется два невыпрямляющих (омических) перехода для соединения полупроводникового кристалла с металлическими выводами. В диоде с выпрямляющим переходом металл-полупроводник имеется один омический переход.

 

Полупроводниковые диоды на основе p-n-перехода

 

Модель структуры диода на основе p-n-перехода изображают, как показано на рис. … (Структура это последовательность областей с отличающимся типом электропроводности). В модели имеются ОПЗ, p-база, n-база и металлизации баз (обозначены штриховкой). Базами называются области кристалла диода вне ОПЗ. Одна из возможных реальных структур кристалла диода имеет,следующий вид (рис…)

 

 

 

VD

На рис.. приведено условное графическое изображение выпрямляющего диода на основе p-n-перехода, которое используется для изображения диода на электрической принципиальной схеме. Диод в схемах именуется, например, как VD5, где 5 – порядковый номер диода в схеме. Кремниевые диоды маркируются следующим образом, например КД212А. Здесь К – кремний, Д – выпрямительный диод, 2 – обозначение класса диода по току или мощности, 12 – код разработки, А – классификационный параметр. Для аналогичного диода в военном исполнении (с военной приёмкой) вместо буквы К используется цифра 2. Например, 2Д212. Маркировка германиевых диодов начинается с буквы Г или цифры 1. Для арсенид-галлиевых – А или 3. Диоды Шотки имеют условное графическое изображение ……..и обозначаются как ……..

 

Идеализированная вольтамперная характеристика диода с широкой базой.

 

Инжекция - введение носителей в область, где они становятся неосновными. Например, введение электронов из n-области в p-область.

Экстракция - введение носителей в область, где они становятся основными. Например, введение дырок из n-области в p-область.

Выведем аналитическое выражение для вольтамперной характеристики диода для случая широкой (толстой) базы, т.е. зависимости тока, текущего через диод, от напряжения приложенного к выводам диода и от параметров структуры диода.

Идеализация заключается в следующем.

1. Диффузионная длина дырок L_p много меньше толщины n-базы W_n, а диффузная длина электронов L_n меньше толщины p-базы W_p, что справедливо для широкой базы.

2. Не учитываются процессы генерации и рекомбинации носителей в ОПЗ.

3. Рассматривается случай малого уровня инжекции (режим малых токов). Это означает, что концентрация инжектированных в n-базу дырок много меньше равновесной концентрации электронов (p_n < n_n0), а концентрация инжектированных в p-базу электронов много меньше равновесной концентрации дырок (n_p < p_p0).

4. Рассматривается плоский, резкий p-n-переход, без учёта краевых эффектов.

5. Полагается равной нулю напряженность электрического поля в базах диода. Это означает, что все приложенное от внешнего источника напряжение падает на ОПЗ. Другими словами, не учитывается сопротивление материала баз, что справедливо для малого уровня инжекции.

6. Не учитываются поверхностная рекомбинация и поверхностные эффекты.

****************** (хорошо бы дать оценку приближений и что-то сказать о диодной и диффузионной теории)

 

Ток в диоде I представляет собой сумму электронной I_n и дырочной I_p компонент.

I = I_n + I_p

Электронная компонента равна произведению заряда электрона на разность потоков электронов пересекающих ОПЗ (**)

 

I_n =e(n_nn-n_np).

При отсутствии напряжения на диоде результирующий поток электронов равен нулю. Следовательно, и I_n равен нулю.

Дырочная компонента равна произведению заряда дырки на разность потоков дырок пересекающих ОПЗ (***)

I_p = e(n_pp- n_pn).

При отсутствии напряжения на диоде результирующий поток дырок через ОПЗ равен нулю. Следовательно, и I_p равен нулю.

Поэтому ток через диод при отсутствии напряжения на его выводах, складывающийся из электронной и дырочной компонент, равен нулю.

Приложим к диоду прямое напряжение (плюсом к p-области и минусом к n-области). Оно уменьшит высоту потенциального барьера (рис..), так как поле внешнего источника направлено противоположно полю контактной разности потенциалов. Зафиксируем положение потенциальных кривых в n-области вне ОПЗ. Тогда потенциальные кривые в p-области снизятся на величину eU по сравнению с равновесным значением. При снижении высоты барьера его начинают преодолевать основные носители с энергией в диапазоне от e(j_к – U) до ej_к, которые не могли его преодолеть в отсутствии внешнего напряжения на диоде. Поток неосновных носителей не изменится, поскольку поле в ОПЗ для них является ускоряющим. В результате потоки основных носителей станут больше, чем встречные потоки неосновных. Поэтому появятся электронная и дырочная компоненты

тока, имеющие одинаковое направление. Следовательно, через диод потечёт ток, который в данном случае называют прямым.

Запишем выражение для потока электронов из n-области, преодолевших барьер:

где U – напряжение на выводах диода.

Умножим и разделим это выражение на 4. Тогда

.

 

В полученном выражении проведём замену

,

тогда поток электронов из n-области (основных носителей) будет равен

.

Рассчитаем поток электронов из p-области (неосновных носителей)

 

.

Определим электронную компоненту тока:

I_n = .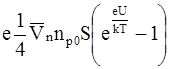

Проведём замену

,

где L_n - диффузионная длина электронов, t_n - время жизни электронов. Тогда выражение для тока будет следующим

I_n = .

Применяя соотношение связи между диффузионной длиной и временем жизни

,

где D_n – коэффициент диффузии, преобразуем выражение для электронной компоненты следующим образом

I_n = .

По аналогии можно записать для дырок

I_p = .

****************************

Тогда ток через диод, равный сумме электронной и дырочной компонент, будет равен

I = I_n + I_p = .

 

Выражение для тока может быть записано следующим образом

 

,

где

называют током насыщения или тепловым током, вследствие его сильной зависимости от температуры.

Если , то можно пренебречь единицей в скобках и характеристика на прямой ветви будет экспоненциальной. Экспоненциальная зависимость тока от напряжения на прямой ветви ВАХ обусловлена экспоненциальной формой распределения носителей по кинетическим энергиям в потоках, падающих на барьер.

В зависимости от материала, из которого изготовлен диод, и его типа величина прямого напряжения находится в пределах от долей вольта до нескольких вольт. Внешнее напряжение лишь частично снижает высоту потенциального барьера.

Обратное напряжение прикладывается минусом к p-области и плюсом к n-области. При приложении обратного напряжения потенциальный барьер в ОПЗ увеличивается, так как электрические поля внешнего источника и контактной разности потенциалов складываются. Энергетическая диаграмма диода при обратном смещении представлена на рис..

Если обратное напряжение по абсолютной величине больше , то можно пренебречь экспонентой в скобках в выражении (**). При этом обратный ток не будет зависеть от напряжения. Это обусловлено тем, что потоки основных носителей, преодолевающих потенциальный барьер, будут намного меньше встречных потоков неосновных носителей, величина которых постоянна и не зависит от напряжения. При любом напряжении поле в ОПЗ для них ускоряющее. Постоянные потоки неосновных носителей создают обратный ток. Концентрация неосновных носителей на несколько порядков меньше, чем основных. Поэтому типичные величины обратных токов в зависимости от материала диода и площади p-n-перехода лежат в диапазоне от наноампер до сотен микроампер. Величины обратных напряжений находятся в пределах от единиц до сотен вольт.

Вольт-амперная характеристика диода представлена на рис.. Она резко несимметрична. При равных по модулю прямых и обратных напряжениях токи на прямой ветви на 6 – 9 порядков больше, чем на обратной. По этой причине к диоду можно приложить обратное напряжение на несколько порядков величины большее, чем в прямом направлении. При этом мощность, рассеиваемая диодом не превышает десятков милливатт. В прямом направлении статическое сопротивление току в диоде намного меньше, чем в обратном. Это обуславливает выпрямляющее свойство диода - проводить ток практически в одном направлении.

Рассмотрим изменение вольт-амперной характеристики с изменением ширины запрещенной зоны. При идентичном легировании контактная разность потенциалов p-n-перехода больше в полупроводнике с большей шириной запрещённой зоны. Рассмотрим график функции распределения в потоке основных носителей, например электронов рис… Он будет одинаков для полупроводников с различной шириной запрещённой зоны, если они легированы одинаково и находятся при одинаковой температуре. В качестве примера рассмотрим диоды, выполненные из германия и кремния. Ширина запрещённой зоны при 300К для германия рана 0,67 эВ, для кремния 1,12 эВ. На рис… пунктиром отмечена высота потенциального барьера для p-n-перехода из кремния ej_кSi и p-n-перехода из германия ej_кGe при отсутствии напряжения на диодах. При приложении к обоим диодам одного и того же прямого напряжения U потенциальный барьер уменьшится на величину eU. При этом результирующий поток электронов, пропорциональный заштрихованной площади под кривой, для кремния (1) окажется меньше, чем для германия (2). Это связано с тем, что носителей с меньшими энергиями, как следует из вида функции распределения, в потоке всегда больше. Следовательно, при равном прямом смещении ток в диоде с меньшей шириной запрещённой зоны будет больше. Поэтому прямая ветвь вольт-амперной характеристики в диодах с меньшей шириной запрещённой зоны идёт выше (рис..).

При обратных напряжениях больших по модулю 3kT/e обратный ток в диодах определяется потоками неосновных носителей:

 

I_s = e(n_np+n_pn) = (1/4) eS(n_p0V_n + p_n0V_p).

 

При прочих равных условиях в диоде, выполненном из полупроводника с большей шириной запрещённой зоны, концентрация неосновных носителей меньше, так как требуется большая энергия для ионизации атомов основного вещества кристалла. В тоже время концентрация фононов, ионизирующих атомы, с ростом энергии убывает. Средние тепловые скорости носителей одного знака в материалах с различной шириной запрещённой зоны практически одинаковы (отличаются из-за различия эффективных масс). Поэтому различия в величинах обратного тока будут определяться концентрацией неосновных носителей. Например, концентрация неосновных носителей в кремнии примерно на три порядка меньше, чем в германии. Поэтому обратные токи в кремниевых диодах примерно на три порядка меньше, чем в германиевых (рис…).*****

Рассмотрим влияние температуры на вольт-амперную характеристику диода. С ростом температуры контактная разность потенциалов уменьшается, то есть уменьшается высота потенциального барьера для основных носителей. Как отмечалось выше, её уменьшение происходит за счёт увеличения концентрации неосновных носителей. Рассмотрим график функции распределения в потоке основных носителей, например электронов, при двух температурах (T2 > T1) рис…. Пунктиром отмечена высоты потенциальных барьеров для обеих температур отсутствии внешнего напряжения на диодах. Для температуры T2 потенциальный барьер ниже. Если при этих температурах к диоду прикладывать одинаковое прямое напряжение U, то потенциальные барьеры будут уменьшаться на величину eU. При этом результирующий поток электронов, пропорциональный заштрихованной площади под кривой, для температуры T1 окажется меньше, чем для температуры T2. Это связано с тем, что носителей с меньшими энергиями, как следует из вида функции распределения, в потоке, падающем на барьер, всегда больше. Следовательно, при равном прямом смещении ток в диоде при большей температуре будет больше. Поэтому прямая ветвь вольт-амперной характеристики при большей температуре идёт выше (рис..).

С ростом температуры экспоненциально растёт концентрация неосновных носителей, а также пропорционально корню из температуры увеличивается скорость носителей в потоке. Поэтому поток неосновных носителей, создающий обратный ток, увеличивается. Следовательно, с ростом температуры обратный ток увеличивается (рис..). Основной вклад в увеличение обратного тока создаёт увеличение концентрации неосновных носителей с ростом температуры.

 

Распределение концентрации инжектированных носителей и

токов в диоде с широкой базой. Условие Шокли

 

При отсутствии напряжения на диоде распределение концентрации носителей в p- и n- областях (вне ОПЗ) по длине диода определяется видом функции распределения концентрации примесных атомов. Для резкого, плоского перехода оно совпадает с распределением примеси. При подаче на диод прямого напряжения инжектированные носители увеличивают концентрацию неосновных носителей в областях структуры, прилегающих к ОПЗ. В диоде с широкими базами по мере диффузии инжектированных носителей в глубину баз происходит их рекомбинация и концентрация инжектированных носителей убывает (рис…). На расстоянии от ОПЗ равном нескольким диффузионным длинам (порядка 3-х) практически все инжектированные неравновесные носители рекомбинируют. На большем расстоянии от ОПЗ концентрация неос новных носителей становится равной равновесной (рис…). Поскольку инжектированные носители нарушают электронейтральность базы, то в базе возникает электрическое поле. Под его действием происходит смещение коллектива основных носителей к инжектированным и введение из металлических выводов основных носителей в количестве равных инжектированному. Таким образом восстанавливается электрическая нейтральность баз. Этот процесс происходит за время диэлектрической релаксации (примерно 10^-12 с.). (Р. Пауль, с. 26) На рис.. представлено распределение концентраций основных и неосновных носителей при прямом смещении на p-n-переходе. Разрывы на осях сделаны, чтобы одновременно изобразить распределение концентраций основных и неосновных носителей, различающихся на несколько порядков.

Градиент концентрации неосновных неравновесных носителей в базах создаёт диффузионный ток. Ток неосновных носителей, протекающий в базах, является преимущественно диффузионным, так как дрейфовый ток неосновных носителей (вследствие малости их концентрации по сравнению с концентрацией основных носителей) пренебрежимо мал. Ток основных носителей в базах является преимущественно дрейфовым. Вследствие большой концентрации основных носителей заряда этот ток обеспечивается весьма малым электрическим полем, которое не оказывает существенного влияния на ток неосновных носителей.

Определим концентрацию неосновных носителей для координат 0 и 0¹. Вначале определим концентрацию дырок. При нулевом напряжении потоки дырок из n-области и p-области в координате 0 равны и противоположно направлены. Сколько дырок поступает в n-базу, столько же и уходит. Поток дырок, преодолевающий барьер при U = 0 равен

При этом концентрация в плоскости с координатой 0 не изменяется и равна p_n0. При приложении прямого напряжения поток дырок из p-области увеличится, а из n-области останется неизменным. Поток будет равен

.

Это приведёт к увеличению концентрации дырок в плоскости с координатой 0.

Свойства распределения по скоростям в потоке таковы, что средняя скорость в потоке носителей, прошедших барьер не меняется. Следовательно, концентрация, как следует из сравнения выражений для потоков, увеличивается в раз:

.

Аналогично на границе 0¹ концентрация электронов при прямом смещении

.

Приведённые соотношения для концентраций на границах ОПЗ называются условиями Шокли. **************(конец л. 4)

Рассмотрим распределение токов в диоде по координате при прямом смещении диода (рис..). Здесь I_pдиф - диффузионный ток дырок в n-базе, I_nдиф - диффузионный ток электронов в p-базе, I_nдр – дрейфовый ток электронов в n-базе, I_pдр – дрейфовый ток дырок в p-базе. Сумма диффузионного и дрейфового токов в любой плоскости сечения перпендикулярной оси абсцисс постоянна (рис..). Диффузионный ток инжектированных в базу носителей непрерывно уменьшается за счёт рекомбинации по мере движения носителей в сторону выводов диода. На расстоянии нескольких диффузионных длин от ОПЗ он равен нулю. Наоборот, дрейфовый ток растет в направлении от границы ОПЗ к выводам диода. В приближении идеального диода токи в ОПЗ не изменяются так, как предполагается, что в ОПЗ нет генерации и рекомбинации.

 

Уравнение непрерывности

 

Уравнение непрерывности устанавливает связь между скоростью изменения концентрации (первой производной концентрации по времени) в каком либо объёме и процессами, вызывающими изменение концентрации. Рассмотрим слой полупроводника n-типа толщиной x площадью S (рис..). Составим уравнение, связывающее скорость изменения концентрации неосновных носителей (дырок) с процессами, вызывающими изменение их концентрации в этом слое.

Изменение концентрации происходит за счёт разности плотностей токов дырок втекающих и вытекающих из этого объёма. Например, если втекающий ток больше вытекающего, то происходит накопление дырок в объёме. Следова тельно, концентрация будет непрерывно увеличиваться. Происходит накопление дырок в слое. Если втекающий ток меньше вытекающего, то концентрация дырок будет уменьшаться. Будет происходить "рассасывание" заряда дырок в слое. Изменение концентрации в объёме также происходит за счёт генерации и рекомбинации подвижных носителей заряда. Уравнение, связывающее скорость изменения концентрации дырок с процессами в слое будет следующим

 

.

Здесь - скорость изменения концентрации, обусловленная разностью плотностей втекающих и вытекающих токов, - скорость уменьшения концентрации, обусловленная рекомбинацией, - скорость увеличения концентрации, обусловленная генерацией носителей тока.

Для большинства типов полупроводниковых приборов, за исключением фотоэлектронных, изменение концентрации, связанное с генерацией, можно не учитывать. Будем считать, что

.

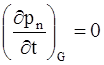При линейной рекомбинации, когда p_n << n_n0 скорость изменения концентрации описывается следующим образом:

.

 

Скорость изменения концентрации за счёт разности плотностей втекающих и вытекающих токов выражается следующим образом

.

Выразим приращение функции плотности тока через дифференциал

 

,

тогда

.

Плотность дырочного тока равна сумме плотностей диффузионной и дрейфовой составляющих

или

.

Тогда

.

С учётом обоих механизмов, вызывающих изменение концентрации имеем нестационарное уравнение непрерывности для дырок

.

По аналогии для электронов уравнение непрерывности имеет вид

.

Для многих случаев величиной напряжённости поля и её производной можно пренебречь.*******************

тогда - нестационарное уравнение непрерывности; - стационарный случай;

- стационарное уравнение напряженности (дырок - электронов);

 

Вывод вольт-амперной характеристики диода на основе

уравнения непрерывности для базы любой толщины

 

 

 

- уравнениение непрерывности для n - базы;

- уравнениение непрерывности для p - базы;

Определим граничные условия:

Введем следующие допущения:

1. Малый уровень инжекции;

2. Генерации и рекомбинации в ОПЗ нет;

3. Диод с плоским p-n-переходом;

4. Электрическое поле в базе отсутствует;

5. Скорость рекомбинации носителей на выводах бесконечна;

Введем новую переменную:

;

Подставим x = 0; Подставим x = W_n;

Получили распределение концентраций в n-базе дырок. Рассмотрим случай широкой (толстой) базы, т.е. W_n>>L_p;

Для случая широкой (толстой) базы:

(Показать на графике распределение для двух значений напряжения)

 

 

 

 

Определим выражение для диффузного тока:

или

.

По аналогии запишем выражение для тока электронов в p-базе для координаты 0^¢:

.

Тогда ток в диоде будет равен сумме токов

 

,

Подставим полученные выражения для токов в координатах 0 и 0^'

.

Отметим, что полученное выражение для тока полностью совпадает с выражением, полученным ранее для идеального диода с толстой базой по балансу потоков.

Рассмотрим случай тонкой базы, когда W_n << L_p, W_p << L_n. Будем определять диффузионный ток дырок в p-базе, а для диффузионного тока электронов в n-базе запишем по аналогии. Полученное ранее выражение для Dp_n(x) имеет вид

.

Поскольку W_n << L_p, то гиперболический косинус аргумента W_n/ L_p близок к 1, а гиперболический синус равен самому аргументу. Поэтому гиперболический котангенс равен

.

Поскольку x < W_n, то неравенство x << L_p более сильное. Поэтому

и .

Подставим значения гиперболических функций в выражение для Dp_n(x):

 

.

На рис… приведены распределения концентрации инжектированных носителей при двух прямых (рис.,а) и двух обратных (рис.,б) напряжениях.

 

 

 

 

 

Линейная зависимость концентрации от координаты получается вследствие не учёта рекомбинации в базе. При прямом смещении можно пренебречь изменением размера базы из-за малости изменения прямого напряжения (доли вольта). При обратных напряжениях (десятки и сотни вольт) изменение размера базы будет заметным.

Продифференцируем распределение концентрации дырок по координате и подставим в выражение для диффузионной составляющей дырочного тока:

.

 

Следует отметить, что величина диффузионного тока при прямом напряжении не зависит от координаты в отличие от случая толстой базы. Это означает, что в стационарном режиме (после окончания переходного процесса) в базе нет дрейфового тока электронов. Последнее следствие того, что в базе практически нет рекомбинации. Рекомбинация инжектированных носителей происходит на металлическом электроде. Поэтому нет необходимости восполнения рекомбинационных потерь электронов в n-базе, которые компенсируют инжектированные дырки, поддерживая электронейтральность базы. Дрейфовый ток течёт только во время переходного процесса.

Запишем очевидное равенство

.

По аналогии можно записать для диффузионного тока электронов в p-базе

.

Величина тока в диоде с тонкими базами, как сумма электронной и дырочной компонент, будет равна

.

Тогда выражение для тока будет иметь вид

или

.

Отметим, что при прочих равных условиях, прямой и обратный токи в диоде с тонкой базой будут больше, чем в диоде с толстой базой, поскольку W меньше L. Кроме этого при обратном напряжении ток будет зависеть от напряжения вследствие зависимости ширины базы от напряжения. За счёт расширения ОПЗ уменьшается размер базы W. Вследствие этого увеличивается градиент концентрации неосновных носителей и, следовательно обратный ток.

 

Вольт-амперная характеристика реального диода

 

Идеализированная вольт-амперная характеристика в целом правильно отражает работу диода при малом уровне инжекции. Однако она не учитывает ряд физических процессов имеющих место в реальном диоде. Поэтому вид вольт-амперной характеристики реального диода будет иметь отличия. Рассмотрим особенности прямой ветви реального диода.

В отличие от идеального диода в реальном диоде протекает ток рекомбинации. Этот ток создают носители, рекомбинирующие в ОПЗ. В основном это носители с энергией меньшей высоты потенциального барьера и не способные преодолеть потенциальный барьер. На рис.. показан механизм протекания тока рекомбинации. Электрон из n-области и дырка из p-области входят в ОПЗ и рекомбинируют в ней, замыкая линии тока.

 

 

 

 

Ток рекомбинации является основной составляющей прямого тока при малых напряжениях в полупроводниках с широкой запрещённой зоной [Дулин, с 68 - 69]. Например, для кремния при напряжениях меньших 0,4 В и температуре 25 ^оС ток рекомбинации больше тока инжекции. При напряжениях больших 0,4 В основной вклад в прямой ток вносит ток инжекции. Для полупроводников с большей шириной запрещенной зоны ток рекомбинации будет больше. Ток рекомбинации пропорционален n_i, а ток инжекции пропорционален n_i², поэтому он менее резко зависит от температуры, чем ток инжекции. С ростом температуры напряжение, при котором эти токи равны, смещается в область меньших напряжений. Ток рекомбинации поднимает начальный участок вольт-амперной характеристики диода (рис..).

 

 

Продолжение следует