PS!Значение 95-процентного квантиляt- распределения c 18 ст.свободы равно 2.1
Значение 95-процентного квантиля F- распределения с 1 и 18 ст.свободы равно 4.413
Задача 2
Данные 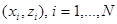 соответствуют модели
соответствуют модели 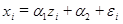 , причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия
, причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия 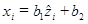 , где ^ означает центрирование.
, где ^ означает центрирование.
а) Пусть вам известны оценки 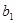 ,
, 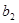 и средние
и средние 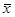 ,
, 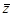 . Найдите по этим данным несмещенные оценки
. Найдите по этим данным несмещенные оценки 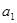 и
и 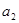 для
для 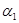 и
и 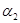 . Поясните свой ответ.
. Поясните свой ответ.
б) Вычислите дисперсию 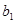 .
.
Задача 3 Расшифруйте формулы и понятия.
| a) b) c) d) e) f) g) h) | а) 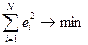 b)
b) 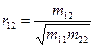 c)
c) 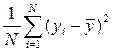 d)
d) 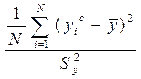 , где , где 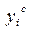 - расчетное значение
e) - расчетное значение
e) 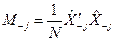 f)
f) 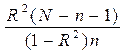 g) Дисперсионное тождество в регрессионном анализе
h)
g) Дисперсионное тождество в регрессионном анализе
h) 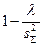
|
Вариант 2 Задача 1=
Для парной регрессии 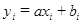 по
по 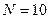 наблюдениям известно, что
наблюдениям известно, что 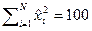 ,
, 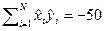 ,
, 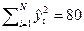 ,
, 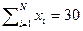 ,
, 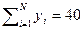 .
.
а) Найдите оценки a, b
б) полную, объясненную и остаточную дисперсии
в) коэффициент детерминации
г) стандартные ошибки параметров регрессии
д) 95- процентные доверительные интервалы для параметров регрессии
е) F -статистику для проверки значимости регрессии в целом. Какой вывод можно сделать?
ж) Пусть в первом наблюдении была ошибка: вместо 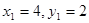 должно было быть
должно было быть 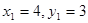 . Пересчитайте коэффициент детерминации с учетом этого исправления.
. Пересчитайте коэффициент детерминации с учетом этого исправления.
PS!Значение 95-процентного квантиляt- распределения c 8 ст.свободы равно 2.306
Значение 95-процентного квантиля F- распределения с 1 и 8 ст.свободы равно 5.32
Задача 2
Данные 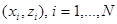 соответствуют модели
соответствуют модели 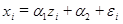 , причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия
, причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия 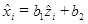 , где ^ означает центрирование.
, где ^ означает центрирование.
а) Пусть вам известны оценки 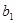 ,
, 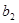 и средние
и средние 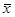 ,
, 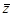 . Найдите по этим данным несмещенные оценки
. Найдите по этим данным несмещенные оценки 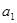 и
и 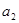 для
для 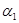 и
и 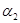 . Поясните свой ответ.
. Поясните свой ответ.
б) Вычислите дисперсию 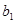 .
.
Задача 3 Расшифруйте формулы и понятия.
| a) b) c) d) e) f) g) h) | а) Какой критерий используется для оценки значимости отдельного фактора регрессии
b) Оценка параметра регресии является несмещенной, если……..
c) 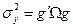 d)
d) 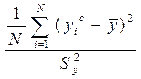 , где , где 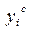 - расчетное значение
e) Сколько степеней свободы имеет статистика Фишера для регрессии с 5-ю факторами и константой, построенной по 25 наблюдениям?
f) - расчетное значение
e) Сколько степеней свободы имеет статистика Фишера для регрессии с 5-ю факторами и константой, построенной по 25 наблюдениям?
f) 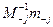 g)
g) 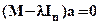 h)
h) 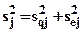
|
Вариант 3 Задача 1--
Для парной регрессии 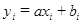 по
по 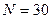 наблюдениям известно, что
наблюдениям известно, что 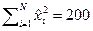 ,
, 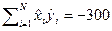 ,
, 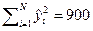 ,
, 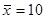 ,
, 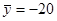 .
.
а) Найдите оценки a, b
б) полную, объясненную и остаточную дисперсии
в) коэффициент детерминации
г) стандартные ошибки параметров регрессии
д) 95- процентные доверительные интервалы для параметров регрессии
е) F -статистику для проверки значимости регрессии в целом. Какой вывод можно сделать?
ж) Пусть в первом наблюдении была ошибка: вместо 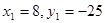 должно было быть
должно было быть 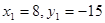 . Пересчитайте a и b с учетом этого исправления.
. Пересчитайте a и b с учетом этого исправления.
PS!Значение 95-процентного квантиляt- распределения c 28 ст.свободы равно 2.048
Значение 95-процентного квантиля F- распределения с 1 и 28 ст.свободы равно 4.21
Задача 2
Данные 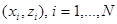 соответствуют модели
соответствуют модели 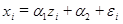 , причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия
, причем выполнены стандартные предположения модели регрессии. По этим данным методом наименьших квадратов оценивается регрессия 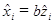 , где ^ означает центрирование.
, где ^ означает центрирование.
а) Пусть вам известна оценка 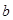 и средние
и средние 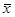 ,
, 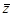 . Найдите по этим данным несмещенные оценки
. Найдите по этим данным несмещенные оценки 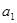 и
и 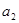 для
для 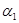 и
и 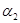 . Поясните свой ответ.
. Поясните свой ответ.
б) Вычислите дисперсию 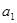 .
.
Задача 3 Расшифруйте формулы и понятия.
| a) b) c) d) e) f) g) h) | а) 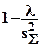 b) Оценка является состоятельной, если……..
c) В каком случае распределение оценки коэффициента регрессии, деленного на его стандартное отклонение, имеет распределение Стьюдента?
d)
b) Оценка является состоятельной, если……..
c) В каком случае распределение оценки коэффициента регрессии, деленного на его стандартное отклонение, имеет распределение Стьюдента?
d) 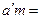 e)
e) 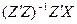 f)
f) 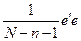 g)
g) 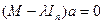 h)
h) 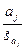
|
Вариант 4 Задача 1;
Для парной регрессии 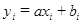 по
по 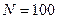 наблюдениям известно, что
наблюдениям известно, что 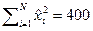 ,
, 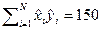 ,
, 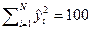 ,
, 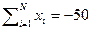 ,
, 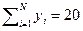 .
.
а) Найдите оценки a, b
б) полную, объясненную и остаточную дисперсии
в) коэффициент детерминации
г) стандартные ошибки параметров регрессии
д) 95- процентные доверительные интервалы для параметров регрессии
е) F -статистику для проверки значимости регрессии в целом. Какой вывод можно сделать?
ж) Пусть в первом наблюдении была ошибка: вместо 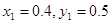 должно было быть
должно было быть 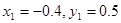 . Пересчитайте объясненную дисперсию с учетом этого исправления.
. Пересчитайте объясненную дисперсию с учетом этого исправления.
P






