Кристалічні тіла характерні тим, що у вузлах кристалічних ґраток перебувають атоми. Атоми здійснюють теплові коливання біля положення рівноваги. Для малих амплітуд ці коливання будуть гармонічними. Енергія кожного атома в кристалі в рівній мірі складається із кінетичної і потенційної енергії, рівних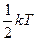 
. Оскільки кінетична і потенціальна енергія атома однакові і в середньому дорівнюють 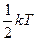, то середнє значення повної енергії, яка приходиться на одну коливальну ступінь вільності буде дорівнювати
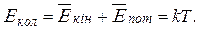(2.7.4)
.
Тепер легко розрахувати теплоємність кристалічної гратки. Для простоти можна вважати, що всі атоми однакові. Кожен атом в кристалі має три ступені вільності. Повна енергія одного вузла відповідно дорівнює 
. Оскільки в одному молі перебуває NА атомів, то внутрішня енергія моля кристалічної речовини буде дорівнювати
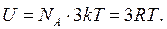(2.7.5)
Теплоємність одного моля кристалічної речовини буде дорівнювати
(2.7.6)
Цей закон був отриманий французькими фізиками Дюлонгом і Пті ще в 1819 році. При низьких температурах закон Дюлонга і Пті не працює. При температурах, вищих за температуру Дебая, закон Дюлонга і Пті дає добрі результати.
Для багатоатомних кристалів молярна теплоємність визначається формулою
(2.7.7)
де n – число атомів у молекулі; R – універсальна газова стала.
Класичні уявлення про внутрішню енергію кристалічної речовини і відповідно теплоємності, не дають пояснення їх залежності від температури. З квантової точки зору при низьких температурах внутрішня енергія атомів в кристалах може набувати лише окремих значень. В цьому випадку кінетична енергія вузлів кристалічної гратки має різні значення для різних ступенів вільності. Енергія одних ступенів вільності стає не суттєвою, енергія інших ступенів вільності стає домінуючою.
Експериментальна залежність молярної теплоємності від температури показана на рис. 2 35.
Рис. 2.35
Графік залежності 
виявився однаковим для різних твердих тіл. Досліджуючи теоретично з позиції квантової теорії внутрішню енергію кристалів, Дебай прийшов до висновку, що внутрішня енергія твердого тіла при температурах, близьких до абсолютного нуля, пропорційна четвертій степені температури
, (2.7.8)
де a – величина, яка залежить від природи кристалів.
Похідна від (2.7.8) визначає молярну теплоємність кристала при низьких температурах
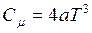. (2.7.9)
Теплоємність, яка визначається за формулою (2.7.8) носить назву закону кубів Дебая.
Для випадку атомної теплоємності коефіцієнт а дорівнює
. (2.7.10)
Атомна теплоємність в цьому випадку буде дорівнювати
, (2.7.11)
де R0 – універсальна газова стала; 
– температура Дебая; T – температура кристалічної речовини.
Закон кубів Дебая добре працює при температурах, нижчих за 
. Вище цієї температури і до температури простої залежності молярної теплоємності від температури поки що не знайдено.
Згідно з теорією Дебая молярна теплоємність для широкого інтервалу температур від нуля до температупи Дебая визначається за формулою
. (2.7.12)
Аналіз формули (2.7.12) показує, що при температурах, близьких до абсолютного нуля, тобто при 
молярна теплоємність буде дорівнювати
(2.7.13)
Цей вираз є законом кубів Дебая. При 
одержуємо закон Дюлонга і Пті.
(2.7.14)
В цьому випадку 
i 
