Найпростішою моделлю молекулярно-кінетичної теорії є модель ідеального газу. У кінетичній моделі ідеального газу молекули уявляються як ідеально пружні кульки, які взаємодіють між собою і зі стінками посудини тільки під час пружних зіткнень. Модель ідеального газу досить добре пояснює поведінку реальних газів у широкому діапазоні тисків і температур. Завдання молекулярно-кінетичної теорії полягає в тому, щоб виявити зв'язок між мікроскопічними параметрами (маса, швидкість, кінетична енергія молекул) і макроскопічними параметрами (тиск, об’єм газу, температура).
У результаті зіткнень молекул між собою і зі стінками посудини, їх швидкості можуть змінюватися як за величиною так і за напрямком. У проміжках між послідовними зіткненнями молекули рухаються рівномірно й прямолінійно. У моделі ідеального газу передбачається, що всі зіткнення молекул є пружними, а тому пояснюються класичними законами механіки Ньютона.
Використовуючи модель ідеального газу, знайдемо тиск газу на стінки посудини. У процесі взаємодії молекул зі стінкою виникають сили, які підпорядковуються 3-му закону Ньютона. Проекція швидкості молекули υx, перпендикулярна до стінки і при взаємодії з стінкою змінює свій знак на протилежний, в той час як проекція швидкості υy, паралельна до стінки і залишається незмінною (рис. 2.9).
Рис. 2.9
У цьому випадку зміна імпульсу молекули буде дорівнює 2m0υx, де m0 – маса молекули.
Виділимо на стінці в напрямку осі х деяку площадку S (рис. 2.10). За час d t із цією площадкою зіткнуться всі молекули, які мають проекцію швидкості υx, спрямовану вбік стінки і перебувають у циліндрі із площею основи S і висотою υxdt.
Якщо концентрація молекул дорівнює n, то їх число в об’ємі виділеного циліндра буде дорівнювати nSυxdt. Але з цього числа молекул лише половина рухається вбік стінки, а інша половина рухається у протилежному напрямку і зі стінкою не стикається. Отже, число зіткнень молекул із площадкою S за час dt буде дорівнювати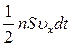 
.
Рис. 2.10
Оскільки кожна молекула при зіткненні зі стінкою змінює свій імпульс на величину 2m0υx, то повна зміна імпульсу всіх молекул, які стикаються протягом часу dt з площадкою S, дорівнює 
. За законами механіки ця зміна імпульсу всіх молекул, що стикаються зі стінкою, відбувається під дією імпульсу сили Fdt, де F ― деяка середня сила, яка діє на молекули з боку стінки в межах площадки S. Але за 3-м законом Ньютона така ж за модулем сила діє з боку молекул на площадку S. Тому можна записати:
S dt. (2.3.3)
Поділивши обидві частини на Sdt, одержимо:
(2.3.4)
де p ― тиск газу на стінку посудини.
У цьому висновку передбачається, що всі n молекул, які містяться в одиниці об'єму газу, мають однакові проекції швидкостей на вісь x. Насправді це не так.
У результаті численних зіткнень молекул газу між собою і зі стінками в посудині, що містить велике число молекул, установлюється деякий статистичний їх розподіл за швидкостями. При цьому всі напрямки векторів швидкостей молекул виявляються рівноправними (мають однакову імовірність), а модулі швидкостей і їх проекції на координатні осі підпорядковуються статистичним закономірностям.
Розподіл молекул газу за модулями швидкостей називається розподілом Максвелла. Максвелл вивів закон розподілу молекул газу за швидкостями, виходячи з основних положень молекулярно-кінетичної теорії. Характерними параметрами розподілу Максвелла є найбільш імовірна швидкість υі, що відповідає максимуму кривої розподілу 
, і середньоквадратична швидкість 
.
З ростом температури максимум кривої розподілу зміщується убік великих швидкостей, при цьому υi і υкв збільшуються.
Щоб уточнити формулу для тиску газу на стінку посудини, маємо припустити, що всі молекули, які містяться в одиниці об'єму, поділені на групи, які містять n1, n2, n3 і т.д. молекул із проекціями швидкостей υx1, υx2, υx3 і т.д. відповідно. При цьому 
. Кожна група молекул вносить свій внесок 
у тиск газу на стінку посудини. В результаті зіткнень із стінкою молекул з різними значеннями проекцій υxi швидкостей виникає сумарний тиск
. (2.3.5)
Алгебраїчна сума, яка входить у цей вираз ― це сума квадратів проекцій υx усіх n молекул в одиничному об’єму газу. Якщо цю суму поді-лити на n, то одержимо середнє значення квадрата проекції υx швидкості молекул 
.
Тепер формулу для тиску газу можна записати у вигляді:
. (2.3.6)
Оскільки усі напрямки для векторів швидкостей молекул мають однакову імовірність, то середні значення квадратів їх проекцій на координатні осі рівні між собою:
(2.3.7)
Остання рівність випливає з формули
. (2.3.8)
Формула для середнього тиску газу на стінку посудини запишеться у вигляді:
. (2.3.9)
Це рівняння встановлює зв'язок між тиском p ідеального газу, масою молекули m0, концентрацією молекул n, середнім значенням квадрата швидкості 
і середньою кінетичною енергією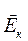 
поступального руху молекул. Його називають основним рівнянням молекулярно-кінетичної теорії газів.
Таким чином, тиск газу на стінку посудини дорівнює двом третинам середньої кінетичної енергії поступального руху всіх молекул, які містяться в одиниці об'єму.
В основне рівняння молекулярно-кінетичної теорії газів входить добуток концентрації молекул n на середню кінетичну енергію 
поступального руху. Якщо припустити, що газ знаходиться у посудині при сталому об'ємі V, то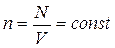 
(N ― число молекул у посудині). У цьому випадку зміна тиску Δp пропорційна зміні 
середньої кінетичної енергії.
Змінювати середню кінетичну енергію руху молекул у посудині при постійному об’ємі можна за рахунок зміни температури. Поняття температури тісно пов'язане з поняттям теплової рівноваги. Тіла, що знаходяться в контакті одне з одним, можуть обмінюватися енергією. Енергія, передана одним тілом іншому при тепловому контакті, називається кількістю теплоти.
Теплова рівновага ― це такий стан системи тіл, які перебувають у тепловому контакті, при якому не відбувається теплопередачі від одного тіла до іншого, і всі макроскопічні параметри тіл залишаються незмінними.
Температура ― це фізичний параметр, однаковий для всіх тіл, що знаходяться в тепловій рівновазі.
Для вимірювання температури використовуються фізичні прилади – термометри, у яких про величину температури судять за зміною якого-небудь фізичного параметра. У різних конструкціях термометрів використовуються різноманітні фізичні властивості речовини (наприклад, зміна лінійних розмірів тіл або зміна електричного опору провідників при нагріванні).
За температурною шкалою Цельсія точці плавлення льоду приписується температура 0° С, а точці кипіння води – 100° С. Зміна довжини стовпчика рідини в капілярі термометра на одну соту довжини між оцінками 0° С і 100° С приймається рівною 1° С. У ряді країн світу широко використовується шкала Фаренгейта (TF), у якій температура замерзаючої води приймається рівною 32° F, а температура кипіння води дорівнює 212° F. Між цими шкалами існує такий зв’язок:
,
або
.
Англійський фізик Кельвін у 1848 році запропонував використовувати точку нульового тиску газу для побудови нової температурної шкали (шкала Кельвіна). У цій шкалі одиниця вимірювання температури така ж, як і в шкалі Цельсія, але нульова точка переміщена:
TК = TС + 273,15.
У системі СІ одиницю вимірювання температури називають кельвіном і позначають буквою K. Температурна шкала Кельвіна називається абсолютною шкалою температур. Вона є найбільш зручною при побудові різних фізичних теорій.
Немає необхідності прив'язувати шкалу Кельвіна до двох фіксованих точок – точки плавлення льоду й точки кипіння води при нормальному атмосферному тиску, як це прийнято в шкалі Цельсія.
Крім точки нульового тиску газу, що називається абсолютним нулем температури, досить прийняти ще одну фіксовану опорну точку. За таку точку використовується потрійна точка води (0,01° С), у якій у тепловій рівновазі знаходяться всі три фази – лід, вода й пара. За шкалою Кельвіна температура потрійної точки води приймається рівною 273,16 К.
З рівняння Менделєєва – Клапейрона одержуємо:
pV = νRT; p = 
; p = n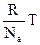 
; p = nkT.
де N – число молекул у посудині; N a – стала Авогадро; n = N / V – концентрація молекул (тобто число молекул в одиниці об'єму посудини); k – деяка універсальна для всіх газів постійна величина. Її називають сталою Больцмана, на честь видатного австрійського фізика Больцмана, одного з творців молекулярно-кінетичної теорії. Стала Больцмана – одна з фундаментальних фізичних констант. Її чисельне значення в СІ дорівнює:
k = 1,38·10–23 Дж/К.
Порівнюючи співвідношення p = nkТ з основним рівнянням молекулярно-кінетичної теорії газів, можна одержати:
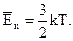(2.3.10)
Середня кінетична енергія хаотичного руху молекул газу прямо пропорційна абсолютній температурі.
Таким чином, температура є мірою середньої кінетичної енергії поступального руху молекул.
Варто звернути увагу на те, що середня кінетична енергія поступального руху молекули не залежить від її маси. Броунівська частинка, зависла в рідині або газі, має таку ж середню кінетичну енергію, як і окрема молекула, маса якої на багато порядків менша маси броунівської частинки. Цей висновок поширюється і на випадок, коли в посудині перебуває суміш газів, що хімічно не взаємодіють, молекули яких мають різні маси. У стані рівноваги молекули різних газів будуть мати однакові середні кінетичні енергії теплового руху, обумовлені тільки температурою суміші. Тиск суміші газів на стінки посудини буде складатися з парціальних тисків кожного газу, тобто
p = p1 + p2 + p3 + … = (n1 + n2 + n3 + …)kT. (2.3.11)
У цьому співвідношенні n1, n2, n3, … – концентрації молекул різних газів у суміші. Це співвідношення пояснює мовою молекулярно-кінетичної теорії експериментально встановлений на початку XIX сторіччя закон Дальтона: тиск у суміші газів, що хімічно не взаємодіють дорівнює сумі їх парціальних тисків.
Лекція 4. Термодинаміка
