Фазовим простором окремого мікростану називають сукупність узагальнених координат і проекцій узагальнених імпульсів на ці координати. Якщо частинки системи розглядати як матеріальні точки, то розмірність фазового простору одного мікростану дорівнює 6, тобто визначається числом трьох координат х, y, z і трьох проекцій імпульсів рx, рy, рz. В цьому випадку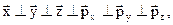 
тобто вектори всіх цих параметрів взаємно перпендикулярні. Для системи із N частинок розмірність фазового простору визначається числом 6N.
Фазовий простір, який відповідає мікростану частинки в одновимірному випадку можна зобразити точкою М (рис. 2.2).
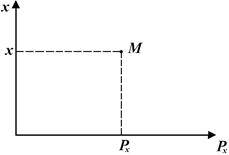
Рис. 2.2
Фазовий простір квантової частинки в одновимірному випадку з урахуванням хвильових властивостей можна зобразити площинкою, сторони якої відповідають невизначеностям Δх і Δрх (рис. 2.3).
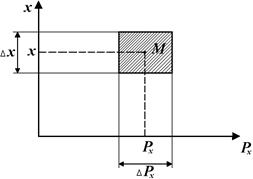
Рис. 2.3
Найменша частина фазового простору, яка відповідає одному мікростану, називається елементарною коміркою фазового простору. В тривимірному випадку елементарна комірка фазового простору має вигляд шестивимірного паралелепіпеда, об’єм якого з урахуванням співвідношень невизначеностей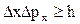 
, 
, 
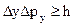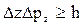, дорівнює
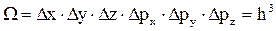, (2.1.8)
де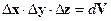 
– об’єм простору, в межах якого перебуває частинка; 
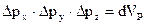– об’єм фазового простору в просторі імпульсів.
В загальному випадку фазовий простір одного мікростану має об’єм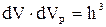 
. Однак в одному мікростані може перебувати кілька квантових частинок. Їх число визначається спіном, тобто в одному мікростані може перебувати 2s+1 частинка (s – спін частинки).
Об’єм фазового простору одного квантового стану менший в 2s+1 рази від об’єму комірки фазового простору
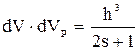, (2.1.9)
де s – спін квантової частинки.
В залежності від спіну квантової частинки в одній елементарній комірці фазового простору одночасно можуть перебувати два електрони (s=½), або три дейтрони (s=1), або один фотон (s=0).
Відомо, що більшість властивостей твердих тіл визначається станом валентних електронів і їх розподілом за енергіями. Розглянемо деяку енергетичну зону валентних електронів. Кількість електронів dN(E), енергія яких перебуває в межах від довільного значення Е до Е+dE прямо пропорційна кількості квантових станів dГ, які відповідають даному інтервалу енергій
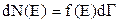, (2.1.10)
де f (E) – функція розподілу, яка відповідає імовірності заповнення відповідних квантових станів частинками.
В свою чергу кількість квантових станів dГ (рис 2.4) пропорційна інтервалу енергій dЕ, тобто
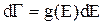, (2.1.11)
де g(E) – густина квантових станів, яка визначає число квантових станів на одиничний інтервал енергії.
В цьому випадку з урахуванням (2.1.10) і (2.1.11) одержуємо:
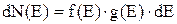(2.1.12)
Рис 2.4
Для визначення числа електронів у виділеній частині енергетичної зони від Е до Е+dЕ слід знати функцію розподілу f (E) і густину квантових станів в цій частині енергетичної зони g(E). З функцією розподілу квантових станів f (E) ознайомимось трохи пізніше.
Густина квантових станів g(E) в загальному вигляді поки не знайдена. Однак для тієї частини енергетичної зони, для частинок якої відомі прості залежності між їх імпульсами й енергіями, густину квантових станів g(E) знаходять із співвідношення (2.1.11)
. (2.1.13)
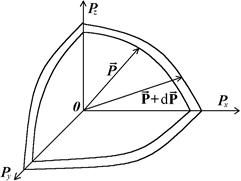
Рис. 2.5
Число квантових станів dГ можна знайти, скориставшись простором імпульсів (рис. 2.5), в якому роль радіуса вектора відіграє вектор імпульсу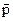 
. Якщо в такому просторі виділити сферичну поверхню радіусом 
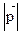з центром в точці 0, то ця поверхня стане геометричним місцем частинок з енергіями Е.
Всі квантові стани з енергіями від Е до Е+dЕ перебуватимуть у тонкому сферичному шарі товщиною dP. Для одержання числа квантових станів dГ слід розділити об’єм виділеного сферичного шару в просторі імпульсів 4πр2dр на об’єм одного квантового стану в просторі імпульсів dVP (2.1.9), тобто
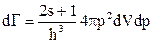. (2.1.14)
Густина квантових станів у цьому випадку буде дорівнювати:
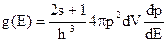, (2.1.15)
де s – спін частинки; р – імпульс частинки; dV – об’єм простору, в якому перебуває частинка;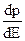 
– проста залежність імпульсу частинок від їх енергії.
Приклади:
а). Густина квантових станів електронного газу в металі.
Для металу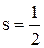 
і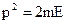 
, тому:
.
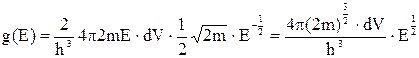б). Густина квантових станів фотонного газу.
Для фотонів s=0 і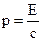 
, де с – швидкість світла, тому:
.
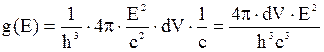