Потоковая контрольная работа фпфэ 2010/2011. По вычислительной математике III курс 5 семестр № группы Фамилия студента оценка Фамилия проверяющего

По вычислительной математике III курс 5 семестр

№ группы	Фамилия студента	Оценка	Фамилия проверяющего

Вариант 5

КВ: Теорема об эквивалентности представления интерполяционного многочлена в форме Лагранжа и в форме Ньютона.

1. (6) Для функции, заданной таблично, найти значение первой производной в указанной точке с максимально возможной точностью.

	x	x 1=0.	x 2=2.	x 3=3.	x 4=5.	x5 =7.
f (x)	–1.	0.	2.	3.	5.

1. (4) Методом обратной интерполяции найти корень нелинейного уравнения, используя приведенные таблицы, оценить точность полученного решения.

	x	x 1=0.5	x 2=0.6	x 3=0.8	x 4=1.
f (x)	–0.378	–0.225	0.103	0.460

1. (4) Методом простой итерации найти ширину функции на полувысоте с точностью 10^-3:

1. (6) Для нахождения положительного корня нелинейного уравнения предложено несколько вариантов МПИ. Исследовать эти методы и сделать выводы о целесообразности использования каждого из них.

1. (4) Для системы нелинейных уравнений указать начальное приближение и описать метод Ньютона для нахождения решения, оценить количество необходимых итераций для достижения точности 10^-5.

1. (6) Для функции, заданной таблично, вычислить значение определенного интеграла методом трапеций, сделать уточнение результата по правилу Рунге. Сравнить уточненный результат с вычислениями по методу Симпсона.

x	x 1=0.	x 2=0.125	x 3=0.25	x 4=0.375	x 5=0.5	x 6=0.625	x 7=0.75	x 8=0.875	x 9=1.
f (x)	0.000000	0.124670	0.247234	0.364902	0.473112	0.563209	0.616193	0.579699	0.000000

1. (5) Предложите метод вычисления несобственного интеграла с точностью 10^-4.

8 *. (5) Пусть A = A ^T>0, и . Доказать, что число обусловленности монотонно убывает по α при α >0.

9 *. (6) Оцените минимальное число узлов, необходимых для вычисления интеграла с точностью ε=10^-2 по методам трапеций, Симпсона и квадратур Гаусса. Вычислите интеграл с заданной точностью любым из этих методов.

10 *. (6) Построить квадратуру Гаусса с двумя узлами для вычисления интеграла .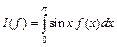

 

 

Ответы к варианту 1

1.

2. x =1.850.

3. Т. Max

6. Это численный интеграл , I _h=1.603144, I _2h=1.596321, I _R=1.605418, I _S=1.605418

9. Ответ. Интегралы подобраны так, чтобы для квадратуры Гаусса было достаточно двух узлов, а по методу трапеций много больше. Точное значение: 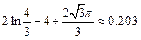, по квадратуре Гаусса:

 

Ответы к варианту 2

1.

2. x =0.213.

3. Т. Max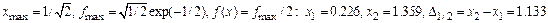

6. Это численный интеграл 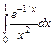, I _h=0.3669885, I _2h=0.371737, I _R=0.365406, I _S=0.365406

9. Ответ. Интегралы подобраны так, чтобы для квадратуры Гаусса было достаточно двух узлов, а по методу трапеций много больше. Приближенное (1000 узлов формулы трапеций): 0.856, по квадратуре Гаусса:

 

Ответы к варианту 3

1.

2. x =0.243.

3. Т. Max

6. Это численный интеграл , I _h=1.519006, I _2h= 1.5429765, I _R= I _S=1.511016

9. Ответ. Интегралы подобраны так, чтобы для квадратуры Гаусса было достаточно двух узлов, а по методу трапеций много больше. Точное значение: , по квадратуре Гаусса: 9/5=1.8

 

Ответы к варианту 4

1.

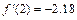
2.x=–0.1054

3. Т. Max

6. Это численный интеграл 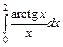, I _h=1.575095, I _2h=1.572338, I _R=1.576014, I _S=1.576014

9. Ответ. Интегралы подобраны так, чтобы для квадратуры Гаусса было достаточно двух узлов, а по методу трапеций много больше. Приближенное (1000 узлов формулы трапеций): 0.923, по квадратуре Гаусса:

 

Ответы к варианту 5

1.

2. x =0.7311

3. Т. Max

6. Это численный интеграл , I _h=0.371127, I _2h=0.334135, I _R=0.383458, I _S=0.383458

9. Ответ. Интегралы подобраны так, чтобы для квадратуры Гаусса было достаточно двух узлов, а по методу трапеций много больше. Точное значение: , по квадратуре Гаусса:

 

 

Для вычисления интеграла используется таблица значений подынтегральной функции:

x	x 1=0.	x 2=0.125	x 3=0.25	x 4=0.375	x 5=0.5	x 6=0.625	x 7=0.75	x 8=0.875	x 9=1.
f (x)	0.909091	1.007266	1.139113	1.278655	1.443376	1.643421	1.889822	2.151657	0.000000

 

Нетрудно посчитать, что подынтегральная функция имеет максимум в точке , и поведение функции на правом краю интервала интегрирования сеточной функцией не прописано. Вычисления методом трапеций дают значение I _h=1.375982, I _2h=1.231714, уточнение по правилу Рунге в точности совпадает с применением метода Симпсона I _S= I _R=1.424071. Довольно муторными выкладками этот интеграл можно вычислить точно, и его значение .

 

Давайте построим решение по алгоритму Рунге-Ромберга на основе экстраполяции вычисленных интегралов в нулевой шаг интегрирования (по h ²) для метода трапеций и метода Симпсона вычисления определенного интеграла.

Метод трапеций:

h 2	I	Δ1	Δ2
(0.5)2=0.25	0.948961
		-1.508016
(0.25)2=0.0625	1.231714		6.697392
		-3.0777173
(0.125)2=0.015625	1.375982

 

Интерполяция в нулевой шаг интегрирования дает I =1.430612, ошибка довольно велика (3,67%).

Метод Симпсона:

h 2	I	Δ1	Δ2
(0.5)2=0.25	1.113765833
		-1.131730222
(0.25)2=0.0625	1.32596525		4.1011788
		-2.092944
(0.125)2=0.015625	1.424072

 

Интерполяция в нулевой шаг интегрирования дает I =1.460779, ошибка вдвое меньше (1,64%), но тоже велика.

Измельчим шаг еще вдвое, при этом впервые появляется единственная точка на убывающем участке функции:

h 2	I	Δ1	Δ2	Δ3
(0.25)2=0.0625	1.32596525
		-2.092944		-79.845679
(0.125)2=0.015625	1.424072		23.7507015
		-3.484586666
(0.0625)2=0.00390625	1.464907

 

Интерполяция в нулевой шаг интегрирования по трем последним шагам дает I =1.479968, ошибка 0,35%.

Интерполяция в нулевой шаг интегрирования по четырем последним шагам дает I =1.480273, ошибка 0,33%. Заметим, что вычисление методом Симпсона даже для самой мелкой сетки дает отличия значительно большие: 1.36%.

 

Интересно сравнить этот результат с интегрированием по Симпсону, когда поведение функции на правом конце учтено еще лучше:

h 2	I	Δ1	Δ2
(0.1)2=0.01	1.442913
		-3.7344000
(0.05)2=0.0025	1.470921		137.78488888
		-5.02613333
(0.025)2=0.000625	1.480345

Интерполяция в нулевой шаг интегрирования дает I =1.483702, погрешность (0,096%).

Теор. Задачи

1. Доказать подчиненность матричной нормы при выборе октаэдрической нормы вектора.
2. Можно ли утверждать, что матрица плохо обусловлена, если определитель матрицы мал?
3. Пусть A = A ^T>0, и . Доказать, что число обусловленности монотонно убывает по α при α>0.
4. Найти область сходимости метода Якоби и метода Зейделя решения СЛАУ A x =f c матрицей

1. Получить формулы односторонней аппроксимации второго порядка производной в точке x=x ₀ по значениям функции в точках x=x ₀, x=x ₁= x ₀+ h, x=x ₂= x ₀+2 h двумя способами; 1) используя интерполянт 2)методом неопределенных коэффициентов.

 

10.* Функция f(x) задана таблицей своих значений в узлах интерполяции

 

x 0= 0.	x 1=1.	x 2=2.	x 3=3.	x 4=4.
1.00000	0.86603	0.50000	0.00000	–0.50000

 

а) Построить кубический сплайн для этой функции, предполагая, что сплайн имеет нулевую кривизну при x=x ₀ и x=x ₄. Вычислить приближенное значение функции в точке x *=1.5.

б) Предложить способ вычисления интеграла от быстро осциллирующей функции

1 вар-т x=1.5

x 0= 0.	x 1=1.	x 2=2.	x 3=3.	x 4=4.
0.00000	0.50000	0.86603	1.00000	0.86603

 

2 вар-т x=0.8

x 0= 0.1	x 1=0.5	x 2=0.9	x 3=1.3	x 4=1.7
–2.3026	–0.69315	–0.10536	0.26236	0.53063

 

3 вар-т x=3.0

x 0= 0.	x 1=1.7	x 2=3.4	x 3=5.1	x 4=6.8
0.00000	1.3038	1.8439	2.2583	2.6077

 

4 вар-т x=0.1

x 0=--0.4	x 1=--0.1	x 2=0.2	x 3=0.5	x 4=0.8
1.9823	1.6710	1.3694	1.0472	0.64350

 

5 вар-т x=1.5

x 0= 0.	x 1=1.	x 2=2.0	x 3=3.0	x 4=4.0
1.00000	1.5403	1.5839	2.0100	3.3464

 

Ответы

1. Отрезок [1,2] a=0.5 b=0.451808 c=–0.0722874 d=–0. 134956 f(x)=0.706145

2. Отрезок [0.5,0.9] a=–0.693147 b=2.72502 c=–4.86964 d=4.32685 f(x)= –0.197082

3. Отрезок [1.7,3.4] a=1.30384 b=0.535474 c=–0.204257 d=0.0447927 f(x)=1.75317

4. Отрезок [–0.1,0.2] a=1.67096 b=–1.02012 c=0885522 d=–0.128102 f(x)=1.46946

5. Отрезок [1.,2.] a=1.54030 b=0.252035 c=–0.432401 d=0.223917 f(x)=1.58621