По вычислительной математике III курс 5 семестр

№ группы	Фамилия студента	Оценка	Фамилия проверяющего

Вариант 3

КВ: Достаточное условие сходимости МПИ для систем нелинейных уравнений.

 

1. (6) Для функции, заданной таблично, найти значение первой производной в указанной точке с максимально возможной точностью.

	x	x 1=0.	x 2=1.	x 3=2.	x 4=3.	x5 =4.
f (x)	4.	2.5	1.	–1.	–2.

1. (4) Методом обратной интерполяции найти корень нелинейного уравнения, используя приведенные таблицы, оценить точность полученного решения.

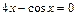
	x	x 1=0.	x 2=0.1	x 3=0.3	x 4=0.5
f (x)	–1.	–0.595	0.245	1.122

1. (4) Методом простой итерации найти ширину функции на полувысоте с точностью 10^-3:

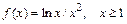
1. (6) Для нахождения положительного корня нелинейного уравнения предложено несколько вариантов МПИ. Исследовать эти методы и сделать выводы о целесообразности использования каждого из них.

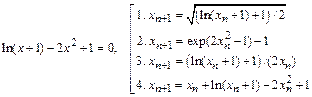
1. (4) Для системы нелинейных уравнений указать начальное приближение и описать метод Ньютона для нахождения решения, оценить количество необходимых итераций для достижения точности 10^-5.

1. (6) Для функции, заданной таблично, вычислить значение определенного интеграла методом трапеций, сделать уточнение результата по правилу Рунге. Сравнить уточненный результат с вычислениями по методу Симпсона.

x	x 1=0.	x 2=0.15	x 3=0.3	x 4=0.45	x 5=0.6	x 6=0.75	x 7=0.9	x 8=1.05	x 9=1.2
f (x)	1.000000	1.007568	1.031121	1.073456	1.140228	1.242129	1.400176	1.660300	2.143460

1. (5) Предложите метод вычисления несобственного интеграла 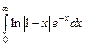с точностью 10^-4.

8 *. (5) Найти 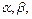при которых методы Якоби и Гаусса — Зейделя будут сходящимися для систем СЛАУ 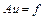с матрицей A вида: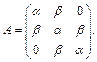

9 *. (6) Оцените минимальное число узлов, необходимых для вычисления интеграла 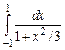с точностью ε=10^-2 по методам трапеций, Симпсона и квадратур Гаусса. Вычислите интеграл с заданной точностью любым из этих методов.

10 *. (6) Построить квадратуру Гаусса с двумя узлами для вычисления интеграла .

 

 

ПОТОКОВАЯ КОНТРОЛЬНАЯ РАБОТА ФПФЭ 2010/2011

По вычислительной математике III курс 5 семестр

№ группы	Фамилия студента	Оценка	Фамилия проверяющего

Вариант 4

КВ: Формулы Ньютона-Котеса 1-го, 2-го и 4-го порядков аппроксимации для интегрирования функций, заданных таблично.

1. (6) Для функции, заданной таблично, найти значение первой производной в указанной точке с максимально возможной точностью.

	x	x 1=0.	x 2=1.	x 3=2.	x 4=5.	x5 =7.
f (x)	1.	0.5	0.3	0.2	0.1

1. (4) Методом обратной интерполяции найти корень нелинейного уравнения, используя приведенные таблицы, оценить точность полученного решения.

	x	x 1=0.5	x 2=0.6	x 3=0.8	x 4=1.
f (x)	–0.229	–0.205	–0.077	0.159

1. (4) Методом простой итерации найти ширину функции на полувысоте с точностью 10^-3:

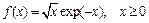
1. (6) Для нахождения положительного корня нелинейного уравнения предложено несколько вариантов МПИ. Исследовать эти методы и сделать выводы о целесообразности использования каждого из них.

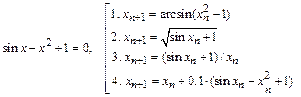
1. (4) Для системы нелинейных уравнений указать начальное приближение и описать метод Ньютона для нахождения решения, оценить количество необходимых итераций для достижения точности 10^-5.

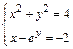
1. (6) Для функции, заданной таблично, вычислить значение определенного интеграла методом трапеций, сделать уточнение результата по правилу Рунге. Сравнить уточненный результат с вычислениями по методу Симпсона.

x	x 1=0.	x 2=0.25	x 3=0.5	x 4=0.75	x 5=1.	x 6=1.25	x 7=1.5	x 8=1.75	x 9=2.
f (x)	1.000000	0.979915	0.927295	0.858001	0.785398	0.716844	0.655196	0.600943	0.553574

1. (5) Предложите метод вычисления несобственного интеграла 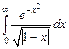с точностью 10^-4.

8 *. (5) Найти 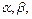при которых методы Якоби и Гаусса — Зейделя будут сходящимися для СЛАУ 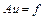с матрицей A вида: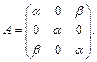

9 *. (6) Оцените минимальное число узлов, необходимых для вычисления интеграла 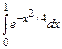с точностью ε=10^-2 по методам трапеций, Симпсона и квадратур Гаусса. Вычислите интеграл с заданной точностью любым из этих методов.

10 *. (6) Построить квадратуру Гаусса с двумя узлами для вычисления интеграла 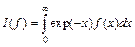.