При расчете на статическую прочность прокатный валок условно представляют как балку, лежащую на двух опорах и загруженную силами и крутящими моментами, причем схема нагружения зависит от типа клети и условий прокатки.
Валки листовых и полосовых станов дуо
Поскольку ширина листа обычно бывает сопоставима с длиной бочки валка, то нагрузку на бочку валка от усилия прокатки Р полагают равномерно распределенной по ширине листа В (q = Р/B) и приложенной симметрично относительно вертикальной оси валка (рис. 2.1).
|
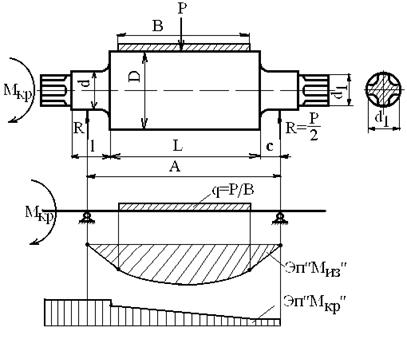
Рис. 2.1. Схема нагружения листового
Валка рабочей клети дуо
изгиб, а шейку - на изгиб и кручение [1-3].
Максимальные напряжения изгиба в бочке валка рассчитывают по формуле
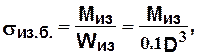 (2.1)
(2.1)
где 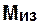 - максимальный изгибающий момент, кН×м;
- максимальный изгибающий момент, кН×м; 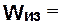 0,1 D3 - момент сопротивления бочки валка изгибу, м 3.
0,1 D3 - момент сопротивления бочки валка изгибу, м 3.
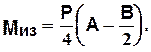 (2.2)
(2.2)
Максимальные изгибающие напряжения в шейке валка возникают по галтели (в месте соединения шейки и бочки валка) и равны:
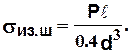 (2.3)
(2.3)
Наибольшие касательные напряжения кручения получаются в приводной шейке валка (см. рис. 2.1) и составляют:
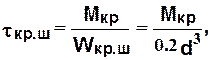 (2.4)
(2.4)
где  - момент сопротивления шейки кручению.
- момент сопротивления шейки кручению.
Суммарное напряжение в шейке определяют в зависимости от материала валка:
- для стальных валков по 4-й теории прочности
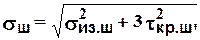 (2.5)
(2.5)
- для чугунных валков по теории Мора
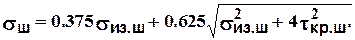 (2.6)
(2.6)
Напряжения в приводной концевой части валка определяют в зависимости от ее формы. Если она выполнена в виде трефа (см. рис. 2.1), то напряжения кручения рассчитывают по формуле
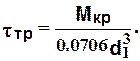 (2.7)
(2.7)
Если концевая часть валка выполнена цилиндрической с шпонкой под съемную головку шпинделя (рис. 2.2,а), то ее рассчитывают также только на кручение по формуле
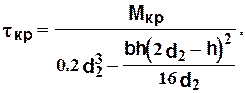 (2.8)
(2.8)
Для концевой части в виде лопасти универсального шарнира (см. рис. 2.2,б) определяют напряжения в двух сечениях. В сечении I-I рассчитывают напряжения изгиба и кручения:
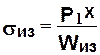 и
и 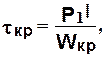 (2.9)
(2.9)
где 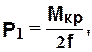

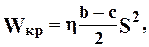
h - коэффициент, учитывающий отношение сторон лопасти и принимающий значение 0.25-0.30 [1].
Суммарное напряжение находят по формулам (2.5) или (2.6) в зависимости от материала валка.
|
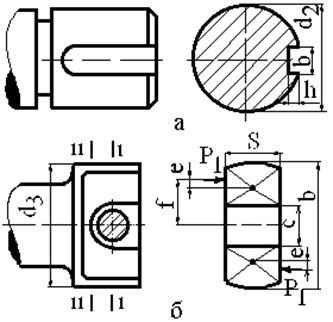
Рис. 2.2. Форма концевых частей
прокатных валков: а - цилиндрическая





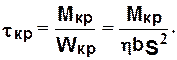 (2.10)
Затем для каждого элемента валка проверяют выполнение условия прочности (1.1) или (1.2).
Численные значения предела прочности валков по нормальным напряжениям
(2.10)
Затем для каждого элемента валка проверяют выполнение условия прочности (1.1) или (1.2).
Численные значения предела прочности валков по нормальным напряжениям  в зависимости от материала приведены в табл. 2.1 [1-3,10].
в зависимости от материала приведены в табл. 2.1 [1-3,10].

