Также известная под названием альфа-ошибка, имеет место тогда, когда по результатам выборочного распределения отклоняют нулевую гипотезу, которая на самом деле верна.
В нашем примере ошибка I рода имела бы место, если мы, исходя из данных выборки,) установили бы, что доля потребителей, предпочитающих новый вид услуг, больше 0,40 (40%), в то время как фактически она была бы меньше либо равна 0,40. Вероятность ошибки I рода (α) также называют уровнем значимости (level of significance).
Уровень значимости (level of significance)
Вероятность ошибки первого рода.
Вероятность ошибки первого рода устанавливается, исходя из допустимого уровняя риска отклонения истинной нулевой гипотезы. Выбор уровня риска зависит от того, во сколько оценивается ошибка первого рода.
Ошибку II рода (Туре II error) совершают, когда, исходя из результатов выборки, не отклоняют нулевую гипотезу, которая в действительности является ошибочной. В нашем примере ошибка II рода имела бы место, если мы, исходя из данных выборки, установили бы, что доля потребителей, предпочитающих новый вид услуг, меньше или равна 0,40, в то время как фактически она была бы больше 0,40. Вероятность ошибки II рода обозначается β. В отличие от α, значение которой устанавливает сам исследователь, величина β зависит от фактического значения параметра генеральной совокупности (например, доли). Вероятность совершения ошибки I рода (α) и вероятность ошибки II рода (β) показаны на рис. 15.4. Вероятность (1 — β) совершения ошибки II рода также называют мощностью статистического критерия.
Рис. 15.4. Ошибка I рода (а) и ошибка II рода (/3)
Ошибка II рода (Type I error)
Также известна под названием бета-ошибка, имеет место тогда, когда результаты выборки ведут к принятию нулевой гипотезы, которая фактически ошибочна.
Мощность критерия (power of a test) представляет собой вероятность (1 — β) отклонения нулевой гипотезы, когда она неверна и должна быть отвергнута. Хотя величина β неизвестна, она связана с α. Чрезвычайно низкое значение α (например, 0,001) приведет к недопустимо высокому значению β. Поэтому необходимо сбалансировать два типа ошибок. В качестве компромисса α часто устанавливают равной 0,05; иногда ей присваивают значение 0,01; другие значения α встречаются редко. Уровень α, наряду с размером выборки, определяет уровень β для конкретного исследовательского проекта. Риском α и β можно управлять, увеличив размер выборки. Для данного уровня значимости а увеличение размера выборки уменьшит значение β, повысив тем самым мощность статистического критерия.
Мощность статистического критерия (power of a test)
Вероятность отклонения нулевой гипотезы, когда она фактически неверна и должна быть отвергнута.
Этап 4. Сбор данных
Размер выборки определяют, приняв во внимание желаемые значения вероятностей совершения ошибок I и II рода и других количественных факторов, например финансовых ограничений. Затем собирают необходимые данные и вычисляют значение выборочной статистики. В нашем примере из 30 опрошенных пользователей Internet 17 отметили, что они приобретают товары через Internet. Таким образом, выборочная доля этих пользователей Internet составляет
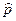= 17/30 = 0,567.
Значение σpможно определить по следующей формуле:
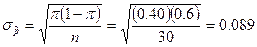
Выборочную статистику z можно вычислить по формуле:
