Эта величина получается делением суммы всех имеющихся значений переменной на число значений.
Среднее арифметическое  задается формулой
задается формулой

где Xi— полученные значения переменной X, п — число наблюдений (размер выборки).
Обычно среднее значение — устойчивый показатель и заметно не изменяется при добавлении или вычитании значений данных. Для частот, представленных в табл. 15.2, среднее арифметическое вычисляют следующим образом:
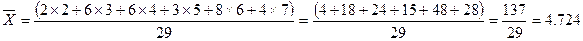
Мода (mode) — значение переменной, встречающееся чаще других. Представляет наивысшую точку (пик) распределения. Мода хороший показатель центра распределения, если переменная имеет категорийный характер, или, иначе говоря, ее можно разбить на категории.
Мода (mode)
Значение переменной, которое чаще всего встречается в выборочном распределении.
Медиана (median) выборки — это значение переменной в середине ряда данных, расположенных в порядке возрастания или убывания. Положение медианы определяется ее номером. Если число данных четное, то медиана равна полусумме двух серединных значений. Медиана — это 50-й процентиль. Она характеризует положение центра распределения порядковых данных. В табл. 15.2 медиана равна 5,000.
Медиана (median)
Значение переменной, которое приходится на середину распределения частот, т.е. одна половина всех значений больше медианы, а другая половина - меньше.
Как видно из табл. 15.2, три показателя, характеризующих положение центра распределения для рассматриваемого нами примера, различны (среднее значение — 4,724; мода— 6,000; медиана — 5,000). И это неудивительно, поскольку каждый показатель определяет центр распределения по-разному. Какой же показатель использовать? Если переменную измеряют по номинальной шкале, то лучше использовать моду. Если переменную измеряют по порядковой шкале, то больше подходит медиана. Если же переменную измеряют по интервальной или относительной шкале, то мода плохо отражает положение центра распределения. Это можно увидеть из табл. 15.2. Хотя значение моды, равное 6,000, отражает наивысшую частоту, оно представляет только 27,6% выборки. Медиана лучше подходит в качестве показателя, характеризующего положение центра распределения, для интервальной или относительной шкалы, хотя и она не учитывает имеющуюся информацию о переменной. Текущие значения переменной до и после медианы игнорируются. Самый лучший показатель для интервальной или относительной шкалы — среднее арифметическое. Он учитывает всю доступную информацию, поскольку для его вычисления используются все значения. Однако среднее арифметическое чувствительно к выбросам значений (экстремально малым или экстремально большим значениям). Если данные содержат выбросы, то среднее не будет хорошим показателем центра распределения и лучше использовать два показателя — среднее и медиану.
Показатели вариации
Показатели вариации (изменчивости) (measures of variability), вычисляемые на основании данных, измеряемых с помощью интервальных или относительных шкал, включают размах вариации, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации.






