(Слайд 11).
Выполнив прямое преобразование, бывает нужно вернуть объект назад. В общем случае это осуществляют посредством обратной матрицы. Если определитель квадратной матрицы не равен нулю, то такая матрица имеет и обратную ей, причём справедливо
Т ∙ Т־¹ = 1.
Обратная матрица считается по известной формуле
А־¹ = 
∙ 
, здесь |А| - определитель матрицы А, число; а матрица преобразования составлена из алгебраических дополнений матрицы А и затем транспонирована.
Для нашего примера матрица обратного преобразования в свёрнутом виде запишется так:
Т־¹ = 
или
слайд 11 – Обратные аффинные преобразования.
Его содержание:
6 Что может подвергаться преобразованиям в геометрических моделях?
Выделим три опорных момента. Подвергать преобразованиям можно
1. Точки. Они задают геометрическую модель как таковую.
2. Направление. Например, надо задать (определить) направление быстро движущегося объекта к точке, находящейся вне поля зрения наблюдателя (за пределом экрана, в большой удалённости от места действия, в ∞-и). На направление влияют только коэффициенты a, b, c и d. Коэффициенты l и m в преобразовании не участвуют, нет точки, которую надо переносить (Слайд 12).
3. Нормали. Это векторы направления перпендикулярные некоторому другому заданному направлению Их преобразование в одной и той же системе координат отличается от преобразования вектора, к которому эта нормаль перпендикулярна. Содержание слайда 12 приведено ниже
· точка (радиус-вектор) (p): 
· вектор (v) и нормаль (n)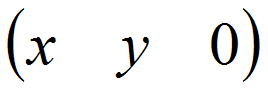 
(только направление, w=0)
Преобразования точек, векторов и нормалей можно записать так
С нормалями всё не так. Это видно из изображения (рис. выше), слайд 12. Базовый объект промасштабирован по оси x в 2 раза и все точки переместились по оси x также в 2 раза. Если это распространить на нормаль, то она станет почти параллельна оси x. А это совсем неверно (на слайде выше показана зелёной стрелкой). В этом частном случае надо нормаль оттянуть назад к оси y. И надо понять – какую матрицу преобразования следует применить к нормали, чтобы выполнить прямое преобразование объекта, сохранив! требуемое направление нормали. На слайде 13 ( ниже приведено его содержание) дан вывод соответствующего преобразования..
Первые три уравнения – есть постановка задачи: а) что известно из теории - скалярное произведение перпендикулярных друг другу векторов равно 0; б) требуется найти матрицу Q преобразования нормали n, если матрица преобразования вектора v – Mtransform известна
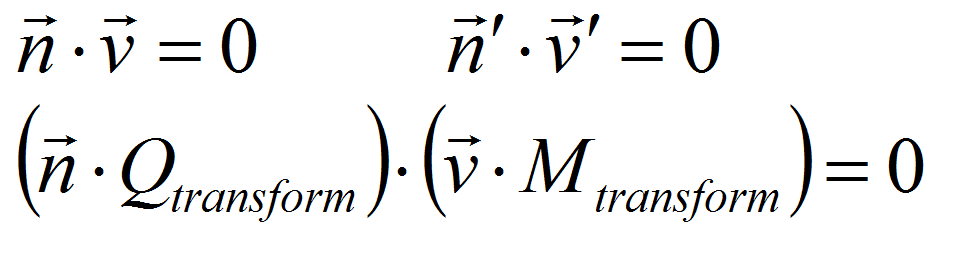
Решение задачи:
Поясним.
Скалярное произведение двух перпендикулярных векторов равно нулю. И оно должно оставаться таким и после преобразования,т.е.:
n ∙ v = 0 и
n' ∙ v' = 0,
Задача состоит в нахождении матрицы преобразования направления нормали, если известна матрица преобразования вектора, к которому эта нормаль перпендикулярна. Известно, что скалярное произведение двух взаимно перпендикулярных векторов равно нулю.
Так как
n' = n ∙ Q transform, а v' = v ∙ M transform,
то (n ∙ Q t ransform ) ∙ (v ∙ MТ transform) = 0
Зададим значения координат для нормали n и вектора v: пусть n = (A, B), а v = (x, y), здесь А и В – координаты вектора нормали; тогда из последней формулы можно составить уравнение, в котором в силу ассоциативности переставлены скобки
(A B 0) ∙ (Q transform ∙ MТ tranмsform) ∙ (x y 0)Т = 0.
Это уравнение справедливо, а так как Q transform ∙ MТ transform = E = 1, то из него найдём
Q transform = (M־¹transform)Т.
Таким образом, для преобразования нормали n одновременно с преобразованием вектора v надо применить не прямую матрицу M преобразования, а ей обратную транспонированную.
Замечание. Варианты нотации записи. Слайд 14. Матрица – это способ хранения информации и в КГ, в программных продуктах уравнения преобразования записывают как вектор-строка умноженная скалярно на матрицу преобразования.
Математики традиционно используют запись через вектор-столбец. Это надо иметь ввиду. С точки зрения логики КГ удобнее писать формулы преобразования как для вектора-строки. Машине же безразлично как эти матрицы составлены.
Если выполняется одно преобразование, то для вектор-строки соответствует первая запись из приведенных ниже, а для вектора-столбца – вторая.
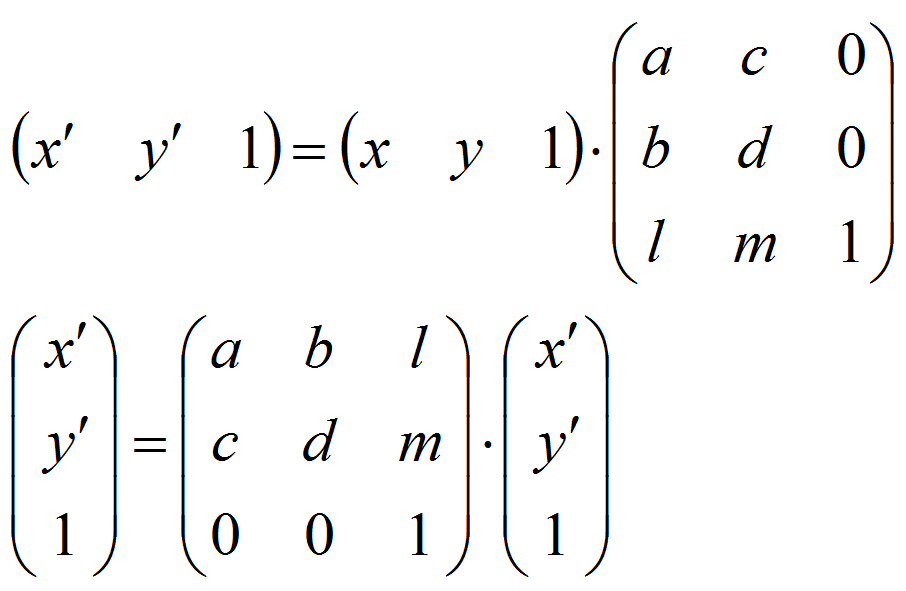
Если выполняется композиция преобразований, то соответственно этому записи имеют вид:
Во второй записи последовательность преобразования обратная действительной последовательности.
