Основной закон динамики поступательного движения (второй закон Ньютона): если на тело массой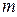 
действует сила 
, то это тело приобретает ускорение 
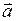, величина которого прямо пропорциональна величине действующей силы и обратно пропорциональна массе данного тела.
Согласно этому закону для какого-либо тела с неизменной массой 
величина ускорения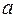 
линейно зависит от величины действующей силы 
, то есть 
. Линейная зависимость величины ускорения от величины действующей силы может быть проверена экспериментально с помощью «машины Атвуда» (рис.1).
 |
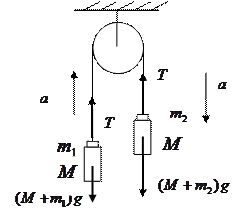Рис.1. Принципиальная схема «машины Атвуда»
Через легкий блок перекинута тонкая нить, на концах которой подвешены грузы массой M каждый. На левый и правый грузы помещают перегрузки массам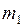и 
и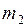 
, причем 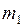¹ 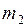(например, 
). В этом случае система грузов массой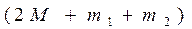 
придет в движение. Результирующая сила, вызывающая ускорение движения этой системы грузов, равна разности сил тяжести перегрузков m1 и m2, лежащих на правом и левом грузах M: 
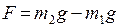. Это выражение справедливо, если пренебречь массой блока и трением в оси блока (в этом случае силы натяжения 
для нитей слева и справа одинаковы по величине). Изменяя массы перегрузков m1 и m2 так, чтобы их сумма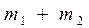 
сохранялась и соответственно сохранялась масса всей системы грузов 
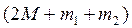, получим несколько значений силы 
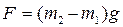, вызывающей ускорение системы. Для каждого значения силы определим ускорение движения 
и найдем зависимость величины 
от величины 
. Величину ускорения грузов можно определить опытным путем с помощью формулы 
, полученной из 
, где h – путь, пройденный телом за время t после начала равноускоренного движения с ускорением 
.
По зависимости величины ускорения для системы грузов массой 
от величины результирующей силы 
проверим справедливость 2-го закона Ньютона.