Исследование изгиба пластин, у которых все кромки жестко заделаны, не может быть проведено с помощью непосредственного применения подстановки М. Леви. Поэтому для решения указанной задачи мы воспользуемся методом наложения и теми зависимостями, которые были получены в § 9 и 10.
Действительно, пластину, жестко заделанную по всем четырем кромкам, можно рассматривать как пластину свободно опертую, но загруженную, помимо заданной внешней нагрузки, еще неизвестными опорными моментами. Если эти моменты будут найдены, то необходимые элементы изгиба пластины определятся суммированием соответствующих элементов изгиба от действия на свободно опертую пластину внешней нагрузки и известных опорных моментов.
Для разыскания неизвестных моментов можно составить нужное число уравнений, если воспользоваться условием, что на жестко заделанных кромках суммарный угол поворота от внешней нагрузки и приложенных моментов должен быть равен нулю.
Рассмотрим частный случай, когда на пластину действует равномерно распределенная нагрузка интенсивностью.
Обозначим опорные моменты, действующие на кромках х = const, М1 и М'1, а моменты на кромках у = const — М2 и М'2 (рис. 36).
Для того чтобы определить углы поворота кромок пластины при действии моментов М1 и М'1, М2 и М'2 разложим моменты М1 и М'1в ряд по синусам аргумента 
, а моменты М2 и М'2 в ряд по синусам аргумента 
(274)
Очевидно, что вследствие симметрии нагрузки и устройства закрепления пластины в разложении (274) следует сохранить лишь нечетные члены.
Воспользовавшись формулами (190), (194), (198), (202), а также формулами (192), (196), (200) и (204) и полагая в них Cn=C'n; Km=K'm (так как вследствие симметрии нагрузки и устройства пластины опорные моменты, действующие на противоположных кромках, будут равны), найдем углы поворота кромок пластины х=0 и у=0 от действия приложенных моментов.
(275)
Углы поворота этих же кромок при действии равномерно распределенной нагрузки определяются формулами (223) и (224)
Приравнивая нулю сумму углов поворота кромок пластины от действующей поперечной нагрузки и опорных моментов, получим следующую систему уравнений:
(276)
Система (276) может быть решена методом последовательных приближений. После определения ряда значений коэффициентов Сn. и Кm вычисление элементов изгиба жестко заделанной пластины сводится к использованию соответствующих формул, выведенных ранее.
Работа, связанная с вычислением элементов изгиба равномерно загруженных прямоугольных пластин, жестко заделанных на опорном контуре, была проделана И. Г. Бубновым, получившим решение этой задачи несколько иным путем.
Представляющие наибольший практический интерес элементы изгиба пластин могут быть вычислены по следующим формулам.
Наибольшая стрелка прогиба (в центре пластины)
(277)
Изгибающие моменты М1 в центре пластины в сечении, перпендикулярном оси ох, и М2 — в сечении, перпендикулярном оси оу
(278)
Наибольший изгибающий момент по середине коротких сторон опорного контура М'1 и по середине длинных сторон опорного контура М'2
Таблица 10
 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
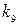
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
3,0
4,0
5,0
| 0,0138 0,0165 0,0191 0,0210 0,0227 0,0241 0,0251 0,0260 0,0267 0,0272 0,0276 0,0279 0,0282 0,0284 0,0284 | 0,0229 0,0234 0,0231 0,0224 0,0215 0,0204 — — — — — — — — 0,0125 | 0,0229 0,0267 0,0302 0,0328 0,0350 0,0368 0,0373 0,0378 0,0389 0,0395 0,0399 0,0405 0,0409 0,0413 0,0417 | 0,0517 0,0491 0,0504 0,0508 0,0511 0,0515 0,0515 0,0515 0,0515 0,0515 0,0515 0,0515 0,0515 0,0515 0,0515 | 0,0517 0,0554 0,0612 0,0668 0,0714 0,0753 0,0784 0,0807 0,0821 0,0826 0,0829 0,0832 0,0833 0,0833 0,0833 | 0,452 0,412 0,381 0,352 0,327 0,305 — — — — — — — — — | 0,452 0,448 0,471 0,491 0,505 0,517 — — — — — — — — — | 0,440 0,450 0,457 0,462 0,464 0,465 0,465 0,465 0,465 0,465 0,465 0,465 0,465 0,465 0,465 | 0,440 0,473 0,493 0,505 0,510 0,515 0,518 0,519 0,520 0,518 0,515 0,510 0,505 0,505 0,500 | 0,250 0,253 0,525 0,256 0,256 0,255 0,255 0,254 0,253 0,252 0,252 0,251 0,251 0,250 0,250 | 0,250 0,271 0,290 0,306 0,320 0,332 0,343 0,352 0,360 0,367 0,379 0,450 0,432 0,450 0,500 |
Перерезывающая сила по середине коротких сторон опорного контура N1 и по середине длинных сторон опорного контура N2
(280)
Наибольшая интенсивность нагрузки коротких сторон опорного контура г1 и длинных сторон опорного контура r2
(281)
Полное давление на короткую сторону опорного контуре R1 и на длинную сторону опорного контура R2
(282)
Входящие в приведенные формулы коэффициенты ki определяются по табл. 10 в зависимости от отношения длинной стороны пластины а к короткой b.
Необходимо отметить следующее. Для рассматриваемой жестко заделанной по всему контуру пластины на кромках. 
, а на кромках 
. Поэтому на основании третьей формулы (137) легко убедиться, что на контуре Н= 0. Следовательно, должно быть г1 = N1 и г2=N2 на контуре, чему противоречат данные табл. 10. Это, по видимому, связано с потерей точности при суммировании медленно сходящихся рядов для третьих производных.
