Ряды.
3.1 Написать пять первых членов ряда по данному общему члену  .
.
Решение. Полагая 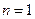 , получаем
, получаем  . Если
. Если 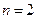 , то
, то  и далее (при
и далее (при 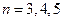 )
)  ,
, 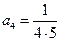 ,
, 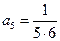 . Следовательно,
. Следовательно,
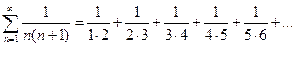
3.2 Написать формулу общего члена для ряда
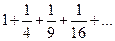
Решение. Знаменатели членов данного ряда – квадраты натуральных чисел, следовательно, общий член ряда
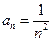 .
.
3.3 Найти для ряда частичную сумму первых n членов (Sn); показать, пользуясь определением, сходимость (расходимость) ряда; найти сумму ряда (S):

Решение. Общий член ряда запишем иначе:
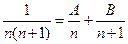 .
.
Определяя коэффициенты А и В, получаем 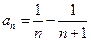 .
.
Следовательно, 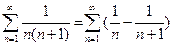 .
.
Напишем частичную сумму ряда
 .
.
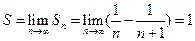 ,
,
отсюда следует, что ряд сходится и его сумма S=1.
3.4 Исследовать сходимость ряда 
Решение: Найдем 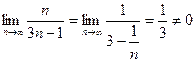 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится.
3.5 Исследовать на сходимость ряд 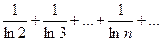
Решение: Т.к. 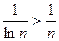 , а гармонический ряд
, а гармонический ряд  расходится, то расходится и ряд
расходится, то расходится и ряд 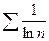 .
.
3.6 Исследовать на сходимость ряд 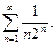
Решение: Т.к. 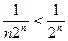 , а ряд
, а ряд 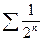 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 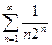 тоже сходится.
тоже сходится.
3.7 Определить сходимость ряда 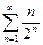 .
.
Решение: Используем признак Даламбера 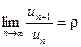
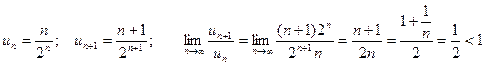
ряд сходится.
3.8 Определить сходимость ряда 
Решение: Используем признак Даламбера 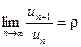

ряд сходится.
3.9 Определить сходимость ряда 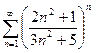 .
.
Решение: Используем признак Коши 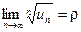

ряд сходится.
3.10 Исследовать по интегральному признаку Коши сходимость ряда:
 .
.
Решение. Пусть y=  –непрерывная, монотонно убывающая и принимающая только положительные значения в интервале (0,
–непрерывная, монотонно убывающая и принимающая только положительные значения в интервале (0, 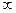 ) функция, причем ее значения, отвечающие целым положительным числам 1, 2, 3,…, совпадают с соответствующими членами
) функция, причем ее значения, отвечающие целым положительным числам 1, 2, 3,…, совпадают с соответствующими членами 
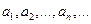 данного ряда. Найдем несобственный интеграл
данного ряда. Найдем несобственный интеграл
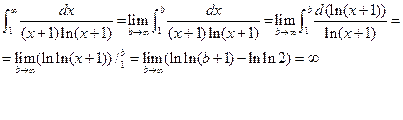
Несобственный интеграл расходится, следовательно, по интегральному признаку данный ряд тоже расходится.
3.11 Исследовать сходимость знакопеременных рядов:
1)  ; 2)
; 2) 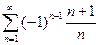 ; 3)
; 3)  .
.
Решение. 1) Члены данного ряда убывают по абсолютной величине, знаки чередуются и общий член с возрастанием n стремится к нулю. Поэтому, согласно признаку Лейбница, ряд 1 сходится. Ряд, составленный из абсолютных величин членов данного ряда
 ,
,
есть гармонический ряд, который, как уже известно, расходится. Следовательно, ряд 1 сходится условно.
2) Члены данного знакочередующегося ряда убывают по абсолютной величине, однако общий член не стремится к нулю с возрастанием n, 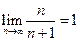 , т. е. необходимое условие сходимости ряда не выполнено, поэтому ряд 2 расходится.
, т. е. необходимое условие сходимости ряда не выполнено, поэтому ряд 2 расходится.
3) Составим ряд из абсолютных величин данного знакопеременного ряда
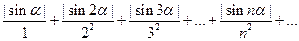 (в)
(в)
Сравним ряд (в) со сходящимся рядом
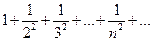 (г)
(г)
Каждый член ряда (в) не превосходит соответствующего члена ряда (г), поэтому, согласно признаку сравнения, ряд (в) сходится. Следовательно, данный ряд 3 сходится абсолютно (безусловно).
3.12 Исследовать на сходимость ряд 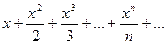
Решение: Применяем признак Даламбера:
 .
.
Получаем, что этот ряд сходится при 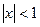 и расходится при
и расходится при 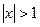 .
.
Теперь определим сходимость в граничных точках 1 и –1.
При х = 1: 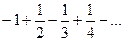 ряд сходится по признаку Лейбница
ряд сходится по признаку Лейбница
При х = -1:  ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
3.13 Найти область сходимости рядов:
1) 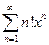 ; 2)
; 2) 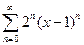 .
.
Решение. 1) 
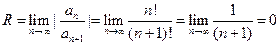 . Ряд сходится только в одной точке x=0.
. Ряд сходится только в одной точке x=0.
2) Положив в данном ряду x-1 =y, получим ряд
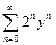 . (a)
. (a)
Найдем радиус сходимости этого ряда:
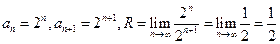 . Исследуем поведение ряда на концах интервала
. Исследуем поведение ряда на концах интервала 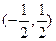 . Пусть y=
. Пусть y= 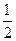 , тогда получим расходящийся ряд
, тогда получим расходящийся ряд 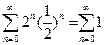 . Пусть y=
. Пусть y=  , тогда получим ряд
, тогда получим ряд 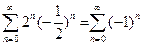 , который также расходится. Следовательно, ряд (а) сходится в интервале
, который также расходится. Следовательно, ряд (а) сходится в интервале 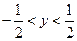 . Заменив переменную y через переменную x, получим искомую область сходимости данного ряда:
. Заменив переменную y через переменную x, получим искомую область сходимости данного ряда:
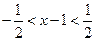 или
или 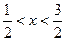 .
.
Элементы гармонического анализа. Ряды Фурье.
3.13. Исследовать на периодичность функцию у = cos 5х + cos 7x.
Решение: Период функции cos5x T1 = 2 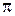 /5, а функции cos7x Т2 = 2
/5, а функции cos7x Т2 = 2 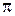 /7.
/7.
Наименьшее число Т, при делении которого на 2 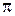 /5 и на 2
/5 и на 2 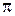 /7 получаются целые числа, есть число 2
/7 получаются целые числа, есть число 2 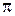 , которое и будет периодом исходной функции.
, которое и будет периодом исходной функции.
Ответ: периодическая, T = 2 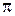 .
.
3.14. Исследовать на периодичность функцию y = sin 3x + sin pх.
Решение: Период функции sin3x T1 = 2 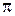 /3, а функции sin
/3, а функции sin 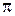 х - T2 = 2
х - T2 = 2 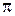 /
/ 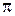 = 2. Однако общего периода у функций sin3x, sin
= 2. Однако общего периода у функций sin3x, sin 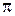 х не существует, поскольку нет числа, при делении которого на 2
х не существует, поскольку нет числа, при делении которого на 2 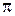 /3 и на 2 получились бы целые числа. Числа 2
/3 и на 2 получились бы целые числа. Числа 2 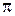 /3 и 2 несоизмеримые.
/3 и 2 несоизмеримые.
Ответ: функция непериодическая.
3.15 Определить период функции y=cos2x. Решение. cos2x=cos2(x+T)=cos(2x+2T), где 2T=2π, т.е. Т=π.
3.16 Разложить в ряд Фурье периодическую функцию 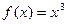 с периодом T = 2p на отрезке [-p;p].
с периодом T = 2p на отрезке [-p;p].
Решение: Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:
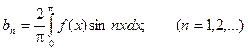
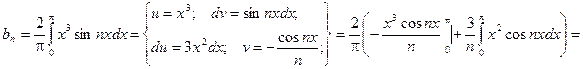
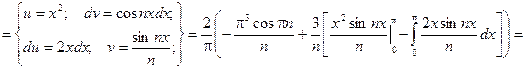
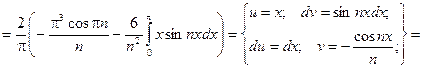
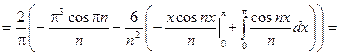

Получаем:  .
.
3.17 Разложить в ряд Фурье функцию
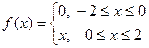 .
.
Решение. Здесь  . Коэффициенты
. Коэффициенты  определяются по формуле (10), а коэффициенты
определяются по формуле (10), а коэффициенты  – по формуле (11), в которых надо вместо
– по формуле (11), в которых надо вместо  подставить 2. Поэтому
подставить 2. Поэтому
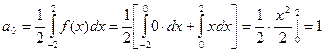 ;
;



Итак, 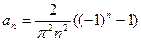 (
(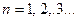 ).
).
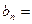


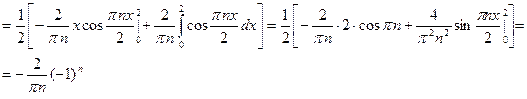
Подставляя найденные значения коэффициентов 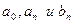 в ряд (9), получим:
в ряд (9), получим:
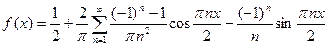 .
.
Теория функции комплексного переменного.
3.18 Записать комплексное число 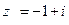 в тригонометрической и показательной формах:
в тригонометрической и показательной формах:
Решение: 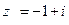 , так как абсцисса отрицательна, а ордината положительна, то точка лежит во второй четверти.
, так как абсцисса отрицательна, а ордината положительна, то точка лежит во второй четверти.
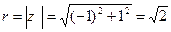 ,
,  , т.е.
, т.е. 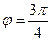 . Поэтому
. Поэтому  .
.
3.19 Комплексное число 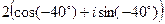 представить в алгебраической форме.
представить в алгебраической форме.
Решение: Здесь 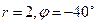 . По формулам
. По формулам  и
и 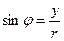 найдем
найдем

Алгебраическая форма данного числа есть (приближенно) 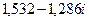 .
.
1.3 Вычислить 
Решение: 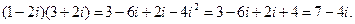
3.20 Вычислить

Решение
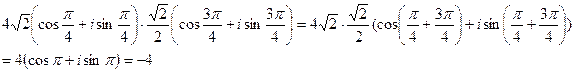
3.21 Найти  .
.
Решение Запишем сначала число  в тригонометрической форме:
в тригонометрической форме:
 ;
; 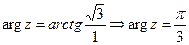 ,
,  .
.
По формуле Муавра имеем
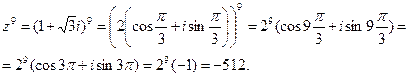
3.22 Найти частное  .
.
Решение:  .
.
3.23 Вычислить 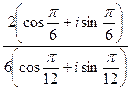
Решение 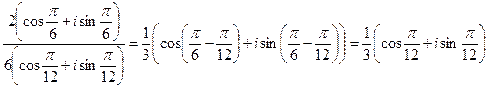
3.24 Найти  .
.
Решение. Запишем подкоренное выражение в тригонометрической форме 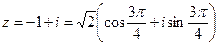 . По формуле
. По формуле
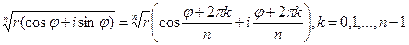
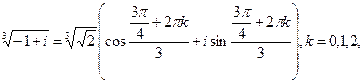
Откуда получаем три значения корня
при 
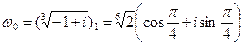 ,
,
при 
 ,
,
при 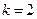
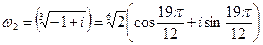 .
.
3.25 Изобразите на рисунке множество точек 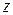 комплексной плоскости, удовлетворяющих условию:
комплексной плоскости, удовлетворяющих условию: 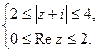
Решение: 1) Запишем z в алгебраической форме 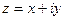 , тогда
, тогда 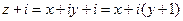 . Найдем
. Найдем 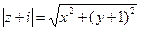 . Тогда
. Тогда
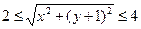 (возведем в квадрат),
(возведем в квадрат),
 .
.
 - окружность с центром
- окружность с центром  и радиусом 2. Неравенство
и радиусом 2. Неравенство 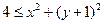 задает множество точек, лежащих за пределами окружности.
задает множество точек, лежащих за пределами окружности.
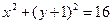 - окружность с центром
- окружность с центром  и радиусом 4. Неравенство
и радиусом 4. Неравенство 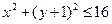 задает множество точек, лежащих внутри окружности.
задает множество точек, лежащих внутри окружности.
2)  , т.е. получаем неравенства
, т.е. получаем неравенства 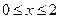 .
.
Решением является пересечение заштрихованных областей.

3.26 Найдите все корни уравнения 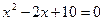 .
.
Решение. 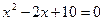 .
.
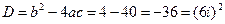 .
.

 .
.
3.27 Найти sin(1+2i).
Решение:
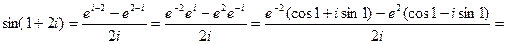
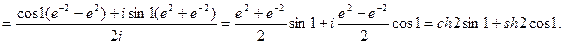
3.28* Найти вычет функции  относительно точки z = 2.
относительно точки z = 2.
Решение: Эта точка является полюсом второго порядка. Получаем:
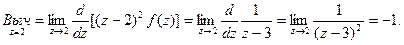
3.29* Вычислить определенный интеграл 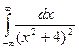 .
.
Решение: Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.
Найдем вычет функции 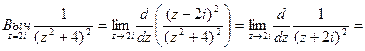
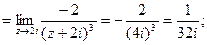
Получаем 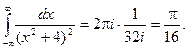
3.30* Вычислить определенный интеграл 
Решение: Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.
Найдем вычет функции
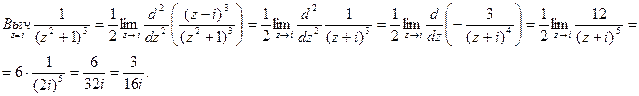 Получаем
Получаем 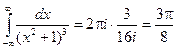
3.31 Восстановить аналитическую функцию по ее действительной и или мнимой части:

Восстановить аналитическую функцию по ее мнимой части можно двумя способами.
Решение.
Первый способ.
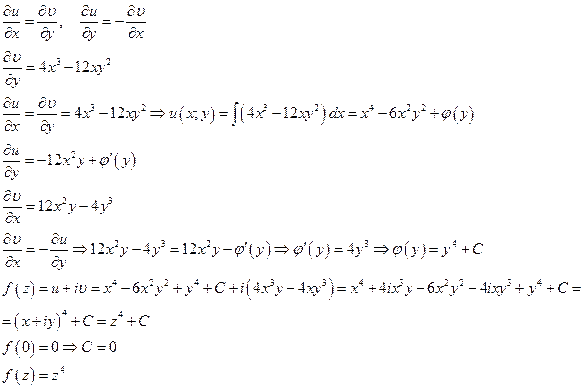
Второй способ.
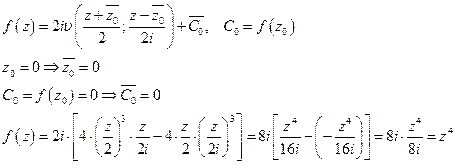
3.32 *.Вычислить:
а) 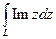 , L – дуга окружности
, L – дуга окружности 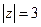 от точки
от точки 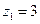 , до точки
, до точки 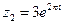
б) 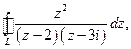
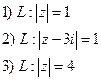
Решение
Теорема Коши о вычетах:
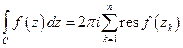
Если точка 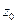 – есть полюс n -го порядка функции
– есть полюс n -го порядка функции  , то
, то
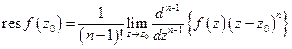
В случае простого полюса 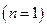

Знаменатель подынтегральной функции обращается в нуль в точках  .
.
1) Внутри окружности  подынтегральная функция аналитическая, поэтому в силу теоремы Коши:
подынтегральная функция аналитическая, поэтому в силу теоремы Коши:
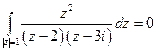
2) Внутри окружности  функция имеет полюс первого порядка
функция имеет полюс первого порядка 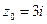 , согласно теореме Коши о вычетах:
, согласно теореме Коши о вычетах:
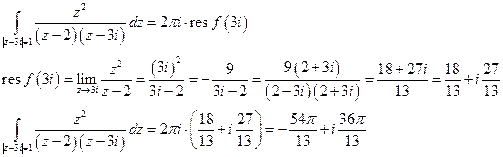
3) Внутри окружности 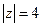 функция имеет два полюса первого порядка
функция имеет два полюса первого порядка 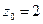 и
и 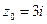 . Согласно теореме Коши о вычетах:
. Согласно теореме Коши о вычетах:

Операционное исчисление.
3.33 Найти оригинал изображения
 .
.
Решение. Представляя изображение в виде 
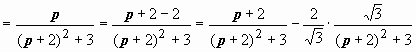 и сравнивая эти выражения с формулами, находим оригинал
и сравнивая эти выражения с формулами, находим оригинал 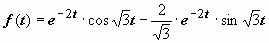 .
.
3.34. Найти оригинал изображения
. 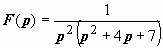 .
.
Решение. Наличие степеней переменной р в знаменателе позволяет применить теорему об интегрировании оригинала: 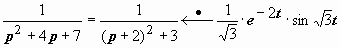 ,
,  ,
,  .
.
Можно решить этот пример с помощью свёртки:
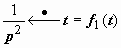 ,
, 
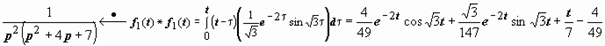 . Однако проще всего представить F (p) в виде суммы простых дробей
. Однако проще всего представить F (p) в виде суммы простых дробей 
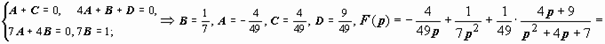

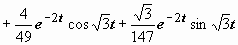
3.35. Найти решение задачи Коши методами операционного исчисления x ″ − 2 x ′ + x = e t, x (0) = 1, x ′(0) = 2.
Решение. Пусть x (t)  X (p).
X (p).
Тогда x ′(t) 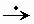 p X (p) − x (0) = p X (p) − 1,
p X (p) − x (0) = p X (p) − 1,
x ″(t) 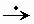 p 2 X (p) − p − 2,
p 2 X (p) − p − 2,
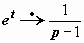 , и изображение задачи имеет вид
, и изображение задачи имеет вид 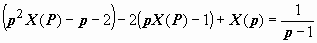 .
.
Находим X (p): 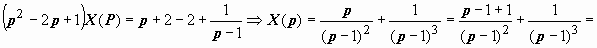
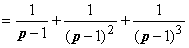 . Обращаем это изображение:
. Обращаем это изображение: 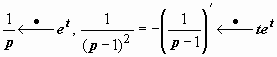 ,
, 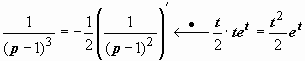 . Решение задачи:
. Решение задачи: 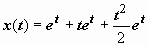 .
.
3.36 Найти решение системы 
удовлетворяющее условиям: x (0) = 1, x ′(0) = 2, y (0) = 0, y ′(0) = 1 при t = 0.
Решение. Пусть x (t) 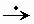 X (p), y (t)
X (p), y (t) 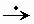 Y (p).
Y (p).
Тогда x ′(t) 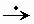 p X (p) − 1, y ′(t)
p X (p) − 1, y ′(t) 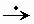 p Y (p),
p Y (p),
x ″(t) 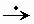 p 2 X (p) − p − 2, y ″(t)
p 2 X (p) − p − 2, y ″(t) 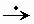 p 2 Y (p) − 1, и изображение задачи имеет вид
p 2 Y (p) − 1, и изображение задачи имеет вид 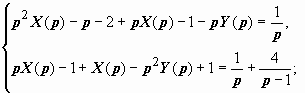

Решаем эту систему относительно X (p), Y (p): из первого уравнения вычитаем второе, умноженное на р: 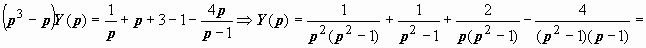 (после разложения на простые дроби)
(после разложения на простые дроби) 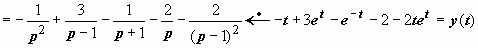 ;
;
Если на р умножить первое уравнение и вычесть второе, получим 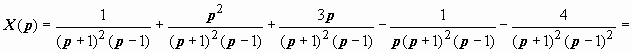
 . Итак, решение задачи
. Итак, решение задачи 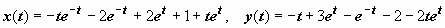 .
.






