Математическое описание транспортного потока

Моделирование транспортного потока. При исследованиях и проек­тировании организации движения приходится прибегать к описанию транспортных потоков математическими методами. Первостепенными задачами, послужившими развитию моделирования транспортных по­токов, явились изучение и обоснование пропускной способности до­рог и их пересечений. Поведение транспортного потока очень измен­чиво и зависит от действия многих факторов и их сочетаний. Наряду с техническими факторами (транспортные средства, дорога) решающее влияние на него оказывают поведение людей (водителей, пешеходов), а также состояние среды движения.

Основы математического моделирования закономерностей дорож­ного движения были заложены в 1912 г. русским ученым, профессором Г. Д. Дубелиром. Первая попытка обобщить математические исследо­вания транспортных потоков и представить их в виде самостоятельно­го раздела прикладной математики была сделана Ф. Хейтом. Дальней­шие исследования и разработки в этой области нашли отражение в ра­ботах многих зарубежных и отечественных ученых.

Известные и нашедшие практическое применение в организации дорожного движения математические модели можно разделить на две группы в зависимости от подхода: детерминированные и вероятност­ные (стохастические).

К детерминированным относятся модели, в основе которых лежит функциональная зависимость между отдельными показателями, напри­мер, скоростью и дистанцией между автомобилями в потоке. При этом принимается, что все автомобили удалены друг от друга на одинаковое расстояние.

Стохастические модели отличаются большей объективностью. В них транспортный поток рассматривается как вероятностный (случайный) процесс. Например, распределение временных интервалов между ав­томобилями в потоке может приниматься не строго определенным, а случайным.

Детерминированные модели. Простейшей математической моделью, описывающей поток автомобилей, является так называемая упрощен­ная динамическая модель. Ее применяют для определения максималь­но возможной интенсивности движения по одной полосе дороги N _{a max} при скорости v _a:

,

(2.2)

где А – коэффициент размерности.

При измерении скорости в километрах в час, а динамического габа­рита в метрах формула (2.2) является выражением для определения про­пускной способности полосы

.

(2.3)

Данная математическая модель составлена на основании двух уп­рощающих допущений: скорость всех транспортных единиц в потоке одинакова; транспортные средства однотипны, т. е. имеют равные ди­намические габариты. Динамический габарит L _а транспортного сред­ства определяют как сумму длины транспортного средства l _а, дистан­ции безопасности d и зазора l ₀ до остановившегося впереди автомоби­ля. Зазор l _о для легковых автомобилей колеблется в пределах 1 – 3 м.

Рассмотрим три применяемых разными авторами подхода к опре­делению динамического габарита L _Д

1. При расчете исходя из минимальной теоретической дистанции безопасности принимают абсолютно равными тормозные свойства пары автомобилей и учитывают только время реакции t _р ведомого во­дителя. Тогда , а уравнение (2.2) приобретает линейный характер. В этом случае возможная интенсивность транспортного по­тока не имеет предела по мере увеличения скорости. Однако это не со­ответствует реальным характеристикам водителей и приводит к завы­шению возможной интенсивности потока. Здесь главную роль играет практическое значительное увеличение t _p при высоких скоростях.

2. При расчете на "полную безопасность" исходят из того, что ди­станция d должна быть равна полному остановочному пути ведомого автомобиля S_o2. Тогда динамический габарит

,

В упрощенной формуле не выделен отрезок, проходимый за время нарастания замедления, а учитывается только установившееся замед­ление j_a. В этом случае уравнение (2.2) приобретает вид квадратичной функции, а интенсивность имеет предел при определенном значении скорости v _a (скорости транспортного потока). Такой подход больше соответствует требованиям обеспечения безопасности движения при высоких скоростях (более 90 км/ч).

3. Наиболее реальный подход основан на той предпосылке, что при расчете дистанции безопасности d надо учитывать разницу тормозных путей (или замедлений) автомобилей, так как "лидер" в процессе тор­можения также перемещается на расстояние, равное своему тормозно­му пути. Более детально это будет рассмотрено в подразделе 2.5.

В результате изучения транспортных потоков высокой плотности и специальных экспериментов, проведенных американскими специали­стами, была предложена теория "следования за лидером", математи­ческим выражением которой является микроскопическая модель транс­портного потока. Микроскопической ее называют потому, что она рас­сматривает элемент потока – пару следующих друг за другом автомо­билей. Особенностью этой модели является то, что в ней отражены за­кономерности комплекса ВАДС и, в частности, психологический ас­пект управления автомобилями. Он заключается в том, что при движе­нии в плотном транспортном потоке действия водителя обусловлены изменениями скорости лидирующего (ведущего) автомобиля и дистан­ции до него в данный момент.

Экспериментальная проверка основного уравнения осуществлялась несколькими учеными методом натурного имитационного эксперимен­та с помощью двух автомобилей, оборудованных аппаратурой для из­мерения значений параметров уравнения. Дистанцию между автомо­билями определяли киносъемкой или специальной амортизирующей лебедкой, которая связывала оба автомобиля. Однако такой экспери­мент уже в своей постановке содержит известную искусственность, ис­кажающую реальный процесс. Это заключается, прежде всего, в специ­альном подборе водителей, автомобилей и задании определенного ре­жима движения. Кроме того, относительно малое число замеров не по­зволяет охватить все многообразие ситуаций, возникающих в реальном транспортном потоке. Дорожные условия и общая транспортная ситу­ация рассматриваются в данной модели не в качестве отдельных пара­метров, а как проявляющиеся в значении скорости движения. Уравне­ние теории следования за лидером описывает взаимодействие между автомобилями с учетом реакции водителя на изменения в транспорт­ном потоке, называемые стимулами.

К моделям, рассматривающим поток в целом и называемым макро­скопическими, относят, например, модели гидродинамической теории.

Наиболее известны две из них, основанные на использовании анало­гии в поведении транспортного потока и потока жидкости. Первая ос­нована на уравнении неразрывности, которое обусловливает постоян­ство количества жидкости при ее протекании по водостоку, и в обозна­чениях, принятых для транспортного потока, в результате преобразо­ваний и упрощений характеризуется зависимостью:

,

где v_a – скорость, подлежащая экспериментальному определению; q_{а mах} – плотность транспортного потока при заторе (v_a = 0).

Вторая гидродинамическая модель использует известное из гидрав­лики понятие о потенциале давления жидкости и предполагает, что дви­жение автомобиля выражается в виде функции некоторого потенциала давления, зависящего от дорожных условий, состояния окружающей среды и психофизиологического состояния водителя.

Стохастические модели. Для решения некоторых задач организации дорожного движения необходимо располагать стохастическими харак­теристиками параметров транспортных потоков в зоне пересечений или на других контролируемых участках дорог. Исследованиями установле­но, что для описания потоков сравнительно малой интенсивности, ха­рактеризующей вероятность проезда определенного числа транспорт­ных средств через сечение дороги, применимо уравнение (распределе­ние) Пуассона

,

(2.4)

где P_n(t) – вероятность проезда n-го числа автомобилей за время t; λ – основной параметр распределения (интенсивность транспортного потока), авт.с; t – длительность отрезков наблюдения, с; n – число наблюдаемых автомоби­лей.

Практически для целей управления движением более необходимо располагать данными о характере распределения временных интервалов между следующими друг за другом транспортными средствами. Если появление автомобилей характеризуется распределением (2.4), то интер­валы между автомобилями распределены по экспоненциальному закону

,

где F(t) – плотность распределения

Следует заметить, что в транспортном потоке физически невозмож­но появление интервалов, меньших, чем соответствующие длине ти­пичного транспортного средства (например, 4 – 5 м для потока легко­вых автомобилей). Поэтому более правильным для описания распре­деления временных интервалов оказывается использование модели смещенного экспоненциального закона:

,

Упомянутые модели совпадают с натурными наблюдениями для однородных потоков, главным образом состоящих из легковых авто­мобилей. При смешанном потоке, а также воздействии некоторых внешних факторов распределение Пуассона не дает удовлетворитель­ных результатов, и в этом случае может быть применено гамма-распре­деление Пирсона III типа или распределение Эрланга.

Движение транспортных средств по дорогам в потоке большой ин­тенсивности и особенно в зоне пересечений может быть рассмотрено на основе теории массового обслуживания. Задачи, решаемые с помо­щью этой теории, обычно сводятся к определению максимального числа "заявок", а также определению очереди в системе по истечении опре­деленного промежутка времени. Применительно к транспортной зада­че это означает возможность определения пропускной способности пересечения, задержек автомобилей и возникающих перед перекрест­ком очередей. Под "заявкой" понимают появление в сечении дороги одного транспортного средства.

При анализе закономерностей дорожного движения, а также при решении практических задач ОДД возникает необходимость исполь­зования взаимозависимостей характеристик транспортного потока. Взаимосвязь интенсивности, скорости и плотности потока на одной по­лосе дороги графически может быть изображена в виде так называемой основной диаграммы транспортного потока (рис. 2.8), отражающей за­висимость

,

Основная диаграмма отражает изменение состояния однорядного транспортного потока преимущественно легковых автомобилей в за­висимости от увеличения его интенсивности и плотности. Левая часть кривой (показана сплошной линией) отражает устойчивое состояние потока, при котором по мере увеличения плотности транспортный по­ток проходит фазы свободного, затем частично связанного и наконец свя­занного движения, достигая точки максимально возможной интенсивности, т. е. пропускной способности (точка N_max = Р_a на рис. 2.8). В процессе этих изменений скорость потока падает – она характеризует­ся тангенсом угла наклона а радиус-вектора, проведенного от точки 0 к любой точке кривой, характеризующей изменение N_a. Соответствую­щие точке N_{a max} = Р_a значения плотности и скорости потока считаются оптимальными по пропускной способности (q_{а опт} и v_{a опт}). При даль­нейшем росте плотности (за точкой Р_а перегиба кривой) поток стано­вится неустойчивым (эта ветвь кривой показана прерывистой линией).

Рис. 2.8. Основная диаграмма транспортного потока: Z – Коэффициент (уровень) загрузки

Переход потока в неустойчивое состояние происходит вследствие несинхронности действий водителей для поддержания дистанции бе­зопасности (действия "торможение–разгон") на любом участке пути и особенно проявляется при неблагоприятных погодных условиях. Все это создает "пульсирующий" (неустойчивый) поток.

Резкое торможение потока (находящегося в режиме, соответствую­щем точке А) и переход его в результате торможений к состоянию по скорости и плотности в соответствующее, например, точке В положе­ние вызывает так называемую "ударную волну" (показана пунктиром АВ), распространяющуюся навстречу направлению потока со скорос­тью, характеризуемой тангенсом угла B. "Ударная волна" является, в частности, источником возникновения попутных цепных столкнове­ний, типичных для плотных транспортных потоков.

В точках 0 и q_{a max} интенсивность движения N_a = 0, т. е. соответ­ственно на дороге нет транспортных средств или поток находится в со­стоянии затора (неподвижности).

Радиус-вектор, проведенный из точки 0 в направлении любой точ­ки на кривой (например, А или В), характеризующей N_a, определяет значение средней скорости потока .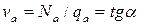

На графике (см. рис. 2.8) показаны для примера две точки, харак­терные: А – для устойчивого движения транспортного потока; В – для неустойчивого, приближающегося к заторовому состоянию потока. Угол наклона радиус-вектора в первой точке а₁ = 60° (tg α= 1,77), а во второй а₂ = 15° (tg α = 0,26). Скорость в точке В(~9,9 км/ч) меньше, чем в точке А (~ 67 км/ч), в 6,8 раза.

Необходимо, однако, отметить, что основная диаграмма не может отразить всю сложность процессов, происходящих в транспортном по­токе, и характеризует его надежно лишь при однородном составе и нор­мальном состоянии дороги и внешней среды. При изменении состоя­ния покрытия, условий видимости для водителей, состава потока, вер­тикального и горизонтального профилей дороги изменяется характер диаграммы. Диаграмма транспортного потока может быть построена и в других координатах, например v _a – q _a и N _a – v _a.