Кинематические и силовые соотношения в передаточных механизмах

 

Кинематические соотношения в передаче можно рассмотреть по схеме цилиндрической фрикционной передачи (см. рис. 1.1, а).

 

Окружная скорость ведущего шкива

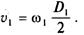
При отсутствии проскальзывания скорость ведущего и ведомого шкивов должна быть одинаковой:

Тогда

Отношение угловой скорости ведущего колеса к угловой скорости ведомого или частоты вращения ведущего колеса к частоте вращения ведомого называется передаточным отношением:

Для передач зацеплением можно использовать следующее выра­жение (поскольку диаметр колеса пропорционален его числу зубьев):

Связь между мощностями на ведущем и ведомом звеньях можно по­лучить из известных формул механики:

 

Известно, что Р = Тω, где Т — вращающий момент; ω — угловая скорость.

Тогда

В зависимости от величины передаточного отношения i передачи делятся на передачи с постоянным передаточным отношением (I /> 1; ω₁ > ω₂ — редукторы, понижающие передачи; I < 1; ω₁ < ω₂ — мультип­ликаторы, повышающие передачи) и передачи с бесступенчатым регу­лированием скорости.

Параллельно с понятием передаточного отношения i используется понятие передаточного числа и\ для редукторов i = и.

В передачах с бесступенчатым регулированием скорости (вариато­ры) передаточное отношение i — величина переменная, и их характери­стикой является диапазон регулирования

Если в механизме необходимо значительное изменение скорости, применяют многоступенчатые передачи.

Ступенью считают передачу одной парой колес, одним ремнем или одной цепью.

На рис. 1.2 изображены многоступенчатые (двухступенчатые) пере­дачи. Нумерация ступеней и колес начинается от двигателя.

Для многоступенчатой передачи общее передаточное число

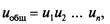
где u₁, и₂, и_n — передаточные числа ступеней.

Общий КПД передачи

где η₁, η₂ и т.д. — КПД ступеней.

Например, для привода, изображенного на рис. 1.2, а, общий КПД

где η _р — КПД ременной передачи; η _ц — КПД цилиндрической зубчатой передачи; η _подш — КПД подшипников.

Для передачи, изображенной на рис. 1.3, можно записать

Скорости валов:

Мощности на валах: Р₂ = Р₁η ₁; Р₃ = Р₂η₂. Вращающие моменты на валах:

Т₂ = T₁u₁, Т₃ = Т₂и₂η₂.