Рассм. интегралы вида ∫R(sinx, cosx)dx, где R - рациональная функция.
Интегралы такого вида берутся с помощью универсальной тригонометрической подстановки: tg(x/2) = t
Выразим sin x, cos x с помощью tg половинного угла, имеем:
 2tg(x/2) 2t
2tg(x/2) 2t
1+tg2(x/2) 1+t2
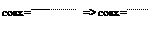 1- tg2(x/2) 1- t2
1- tg2(x/2) 1- t2
1+tg2(x/2) 1+t2
|
 2dt
2dt
1+t2

|
1+t2 1+t2 1+t2
Частные случаи подстановок.
Рассм. подстановки, кот. быстрее приводят к цели в нек. случаях, чем предыдущая подстановка.
1. ∫R(sinx, cosx)dx, где R – нечетная ф-я относ-но sin х, тогда делаем подстановку cos x = t и под знаком ∫ выполняем все действия, заменяя х на t.
2. Если R- нечетная ф-я относ. cos x, то sin x = t.
3. ∫simmx * cosnx dx
а) из m, n – явл. нечетными, если n- нечетное, то примен. подстановка х=t. Если m – нечетное, то примен. подстановка cos x = t.
б) оба показателей m, n – четные полож. числа. В этом случае степень подынтгр. выраж-я пониж. С помощью тригон. ф-л:
sin2x = (1-cos2x)/2, cos2x = (1+cos2x)/2, sinx * cosx = 1/2 sin2x






