Теорема Лагранжа. Если f (x) непрерывна на отрезке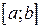 
и дифференцируема во всех его внутренних точках, то найдется хотя бы одна точка 
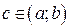, для которой выполняется равенство: 
.
Теорема Ролля. Между двумя различными корнями дифференцируемой функции содержится, по меньшей мере, один корень её производной.
Геометрическая иллюстрация приведена на рисунке:
если a, b – нули функции, т.е. 
и 
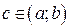, то существует точка такая, что 
, т. е. с – ноль производной 
.
Геометрическая интерпретация теоремы Ролля. Пусть f (x) непрерывна на отрезке 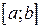, дифференцируема во всех его внутренних точках 
и принимает на концах отрезка одинаковые значения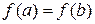 
. Тогда существует по крайней мере одна точка 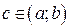, в которой производная функции равна нулю: .
Геометрическая иллюстрация приведена на рисунке:
если f (x) дифференцируема и 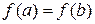, то найдется хотя бы одна точка 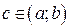, в которой касательная горизонтальна.
Теорема Коши. Если 
и 
– две функции, непрерывные на отрезке 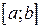и дифференцируемые в интервале 
, причём 
для любого , то между а и b найдётся такая точка с, что 
.
----------------------------------------------------------------------------------------------------------------
Дифференциал функции. Стр. 2
