Цикл for

Цикл for, наиболее универсальный из всех циклов языка С, выглядит так:

for ([инициализация]; [условие]; [модификация]) оператор

Прежде всего выполняется инициализация цикла; секция инициализации может содержать любое выражение. Инициализация производится только один раз перед началом работы цикла. Оценивается выражение условия. Если оно истинно, выполняется оператор тела цикла; если условие ложно, происходит выход из цикла и управление передается следующему оператору.

После исполнения тела цикла производится модификация, после чего управление возвращается заголовку цикла и все повторяется снова. Секция модификации может содержать любое выражение; обычно в ней изменяют значения управляющих переменных цикла.

Как видно из синтаксического описания, любую секцию заголовка цикла for можно опустить, но разделители — точки с запятой — все равно должны присутствовать.

Если опущено условие, цикл будет выполняться бесконечно. Простейшей и самой популярной конструкцией на основе цикла for является цикл с управляющей переменной-счетчиком:

int i;

for (i =0; i < REPEAT; i++)

DoSomething (i);

Счетчик инициализируется значением 0. В начале каждого прохода цикла проверяется, не достиг ли он значения REPEAT. Как только i станет равным REPEAT, тело цикла пропускается и управление передается следующему оператору. В конце каждого прохода i увеличивается на единицу [1].

Любую конкретную структуру повторения, требуемую для решения некоторой задачи, можно реализовать на основе любого из циклов С, однако всегда какой-то из них подходит к данному случаю наилучшим образом, позволяя написать более ясный и компактный код. Так, если необходимое число итераций цикла известно заранее (как при обработке массива), проще всего применить цикл for. Если же число итераций заранее определить нельзя, как в нашем примере обработки команд (момент завершения цикла определяется пользователем) или при операциях поиска в списке, применяют цикл while или do...while.

У структур повторения в ряде ситуаций есть альтернатива. Это рекурсия, заключающаяся в том, что функция вызывает саму себя. Естественно, такой вызов должен быть условным, т. е. обязательно должен наступить такой момент, когда на очередном шаге рекурсивного вызова не происходит. Есть классический пример рекурсии — вычисление факториала:

unsigned Fac(unsigned n)

{

if (n)

return n * Fac(n - 1);

else

return 1;

}

Пример 1. Протабулировать функцию в заданном интервале [2,3] с шагом 0,1 [3].

1. Поместите на форму объекты: Edit1, Edit2, Edit3, Label1, Label2, Label3, Memo1, Button1, Button2.

2. Присвойте объектам свойства согласно таблице:

Объект	Свойства	Значение
Edit1	Text	‘’
Edit2	Text	‘’
Edit3	Text	‘’
Label1	Caption	A=
Label2	Caption	B=
Label3	Caption	H=
Memo1	Lines	‘’
Button1	Caption	Выполнить
Button2	Caption	Выход

3. Дважды щёлкнув по кнопке “Выход”, впишите в месте, где мигает курсор

Close();

4. Дважды щёлкнув по кнопке “Выполнить”, впишите следующий код:

5. Сохраните проект в папке и выполните его.

Пример 2. Найти минимальное и максимально значение данной функции в заданном интервале: [2; 3].

1. Поместите на форму объекты: Edit1, Edit2, Edit3, Label1, Label2, Label3, Memo1, Button1, Button2.

2. Присвойте объектам свойства согласно таблице:

Объект	Свойства	Значение
Edit1	Text
Edit2	Text
Edit3	Text
Edit4	Text
Edit5	Text
Label1	Caption	A=
Label2	Caption	B=
Label3	Caption	H=
Label4	Caption	Max
Label5	Caption	Min
Button1	Caption	Выполнить
Button2	Caption	Выход

3. Дважды щёлкнув по кнопке “Выход”, впишите в месте, где мигает курсор

Close();

4. Дважды щёлкнув по кнопке “Выполнить”, впишите следующий код:

5. Сохраните проект в папке и выполните его.

Результат выполнения программы:

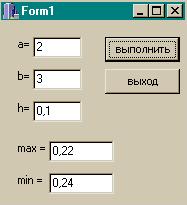
Контрольные вопросы

1. Какие операторы цикла вы знаете?

2. Когда используется оператор цикла ДЛЯ?

3. Как изменяется управляющая переменная в цикле ДЛЯ?

4. Когда применяется составной оператор в цикле?

5. Когда выполняется тело оператора цикла ПОКА?

Вариант задания	Уравнение	Отрезок	Шаг
	e^x- e^-x-2 = 0	[0;1]	0.1
	3sin +0.35x - 3.8 = 0	[2;3]	0.1
	x – 2 +sin(1/x) = 0	[1.2,2]	0.1
	1 – x + sinx - ln(l+x) = 0	[0;1.5]	0.1
	x²– ln(1+x) – 3 = 0	[2;3]	0.1
		[0,0.85]	0.1
	Lnx – x + 1.8 = 0	[2;3]
		[1;2]	0.1
	x + cos(x^0.52+2) = 0	[0.5;1]	0.05
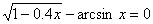
		[0;1]	0.01
		[0;1]
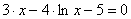
		[2;4]	0.15
		[1:2]	0.1
		[0;1]	0.1
	2x-31nx-3=0	[0.5;0.6]	0.01

Задание №2. Найти min и max значения данной функции в заданном интервале.