Двоично-троичный словарь

Бинарное дерево называется полностью сбалансированным, если оба его поддере­ва имеют примерно одинаковую высоту (или размер) и также являются сбалансиро­ванными. Высота сбалансированного дерева приблизительно равна leg n, где п -• количество узлов в дереве. Время, необходимое для вычисления отношений in, add и delete на бинарных словарях, возрастает пропорционально высоте дерева. Поэтому все эти операции на сбалансированных словарях могут быть выполнены за время, пропорциональное log я. Логарифмический рост затрат времени на проверку при­надлежности к множеству представляет собой значительное улучшение по сравнению со способом представления множеств в виде списков, при котором затраты времени растут пропорционально размеру набора данных. Но если дерево плохо сбалансиро­вано, эффективность доступа к словарю снижается. Б крайних случаях бинарный словарь вырождается в список, как показано на рис. 10.1. Форма словаря зависит от того, в какой последовательности в него вставлялись данные. В лучшем случае обес­печивается хорошая сбалансированность, при которой эффективность доступа про­порциональна log n, а в худшем случае эффективность доступа пропорциональна п. Анализ показывает, что в среднем, при условии, что любая последовательность ввода данных является равновероятной, эффективность выполнения отношений in, acid ж delete все равно остается пропорциональной log n. Поэтому, к счастью, эффектив­ность в среднем ближе к наилучшему, чем к наихудшему случаю. Но существуют и другие довольно простые схемы обеспечения хорошей сбалансированности дерева не­зависимо от последовательности данных. Такие схемы гарантируют эффективность

выполнения отношений in, add и delete, даже в худшем случае пропорциональную log n. Одной из них являются двоично-троичные (сокращенно 2-3) деревья, а дру­гой - AVL-деревья.

Двоично-троичное дерево определяется следующим образом. Оно является либо пустым, либо состоящим из единственного узла, либо представляет собой дерево, ко­торое соответствует следующим условиям.

• Каждый внутренний узел имеет два или три дочерних узла.

• Все листья находятся на одном и том же уровне.

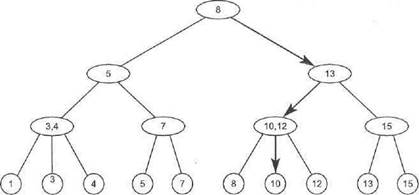
Двоично-троичный словарь представляет собой двоично-троичное дерево, в кото­ром элементы данных хранятся в листьях, упорядоченных слева направо. (Пример такого дерева приведен на рис. 10.2.) Внутренние узлы содержат метки, которые обозначают минимальные элементы поддеревьев следующим образом.

• Если внутренний узел имеет два поддерева, то он содержит минимальный эле­мент второго поддерева.

• Если внутренний узел имеет три поддерева, то он содержит минимальные эле­менты второго и третьего поддеревьев.

Рис. 10.1. Полностью несбалансирован­ный бинарный словарь; эффективность доступа к нему снижается до уровня эффективности доступа к списку

Рис 10.2. Двоично-троичный словарь; указанный путь соответствует по­следовательности поиска элемента 10

216 Часть I.Язык Prolog

Для поиска элемента X в двоично-троичном словаре необходимо начинать с корня и переходить на нижний уровень, руководствуясь метками на внутренних узлах. Предположим, что корень содержит метки Ml и М2, В таком случае должны выпол­няться следующие действия:

• если X < Ml, то продолжать поиск в левом поддереве;

• иначе, если X < К2, то продолжать поиск в среднем поддереве;

• иначе продолжать поиск в правом поддереве.

Еще один вариант состоит в том, что корень содержит только одну метку, К. В таком случае, если X < М, то поиск должен продолжаться в левом поддереве, а иначе — в правом поддереве. Такие операции поиска продолжаются до тех пор, пока не будет достигнут уровень листьев, и в этот момент либо успешно обнаруживается элемент X, либо поиск завершается неудачей.

Поскольку все листья находятся на одном и том же уровне, двоично-троичное де­рево является идеально сбалансированным по отношению к значениям высоты своих поддеревьев. Все пути поиска от корня до любого листа имеют одинаковую длину, пропорциональную log л, где п — количество элементов, хранящихся в дереве.

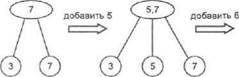
При вставке новых данных двоично-троичное дерево может также расти в шири­ну, а не только в глубину. Каждый внутренний узел, имеющий два дочерних узла, может включить дополнительный дочерний узел, что приводит к росту дерева в ши­рину. С другой стороны, если узел с тремя дочерними узлами принимает еще один дочерний узел, то разделяется на дна узла, каждый из которых принимает два до­черних узла из общего количества, равного четырем. Созданный таким образом но­вый внутренний узел вставляется в дерево на более высоком уровне. Бели это проис­ходит на самом верхнем уровне, то возникает необходимость увеличить количество уровней дерева. Описанные выше действия проиллюстрированы на рис. 10.3.

 

Рис. 10.3. Вставка элементов е двоично-троичный словарь; береоо вначале растет в ширину, а затем — в высоту

Операцию вставки элементов в двоично-троичный словарь можно запрограммиро­вать как следующее отношение; add23(Tree, X, NewTree)

где NewTree — дерево, полученное в результате вставки элемента X в дерево Tree. Основная работа но вставке элементов будет передана двум вспомогательным отно­шениям, которые оба именуются как ins. Первое из них имеет следующие три па­раметра:

ins* Tree, X, NewTree)

где NewTree - результат вставки X в дерево Тгоо. Деревья Tree и NewTree имеют одинаковую высоту. Но, безусловно, не всегда возможно сохранить после вставки прежнюю высоту. Поэтому предусмотрено еще одно отношение ins с пятью парамет­рами, позволяющее учесть эту ситуацию, следующим образом:

ins (Tree, X, NTa, Mb, HTb}

В данном случае после вставки элемента X в дерево Tree последнее разделяется на два дерева, NTa и NTb, имеющие такую же высоту, как и Tree. Здесь Mb является минимальным элементом дерева NTb. Пример ситуации, в которой дерево необходимо разбить на два, показан на рис. 10.4.

Глава 10. Усовершенствованные методы представления деревьев 217

NTa

Mb 6

NTb

Рис. 10.4. Пример, в котором объекты соответствуют отношению ins ( Tree, 6, NTa, Mb, NTb}

В разрабатываемой программе двоично-троичное дерево должно быть представле­но, в зависимости от его формы, следующим образом.

• nil представляет пустое дерево.

• 1 (X) представляет дерево с одним узлом — листом с элементом X.

• п2 (Т1, к, Т2) представляет дерево с двумя поддеревьями, Т1 ит2; М — ми­нимальный элемент Т2.

• пЗ(Т1, М2, 12, МЗ, ТЗ) представляет дерево с тремя поддеревьями, Tl, T2 и ТЗ; М2 - минимальный элемент Т2, а МЗ - минимальный элемент ТЗ.

Здесь Tl, T2 и ТЗ являются двоично-троичными деревьями.

Отношение между add23 и ins характеризуется тем, что если после вставки эле­мента дерево не растет вверх, то имеет место следующее правило:

add2 3(Tree, X, NewTree):-ins (Tree, X, NewTree).

Но если высота дерева после вставки увеличивается, то отношение ir-.s определяет два поддерева, 71 и 72, которые затем объединяются в более крупное дерево:

add23[ Tree, X, п2 (Tl, М, 72) ):- ins С Tree, X, Tl, И, Т2).

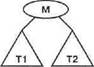
Отношение ins является более сложным, поскольку в нем должно учитываться много вариантов: вставка в пустое дерево, а дерево с одним узлом, в дерево типа:.2 или пЗ. Дополнительные промежуточные варианты возникают в результате вставки в первое, второе или третье поддерево. Соответственно, отношение ins определено как набор правил таким образом, что в каждом предложении, касающемся ins, рассмат­ривается один из вариантов. Некоторые из этих вариантов приведены на рис. 10.5. Варианты, показанные на данном рисунке, можно представить на языке Prolog сле­дующим образом.

Вариант А

ins(n2 I Т1, M, 12) X, п2(NT1,

gt(М, X), ins(Tl, X, NT1].

М, Т2)):-

% М Больше чем

X

Вариант Б

.ns(п2(Tl, К, Т2», X, лЗ(NTla, Mb, HTlb, К, Т2) }:-

gt{ и,:■::,

ins{ Ti, X, NTla, Mb, NTlb].

Вариант В

ins (ri3 (Tl, H2, T2, МЗ, T3], X, n2 (NTla, Mb, NTlb), Ш gt£ M2, X), ins(Tl, X, NTla, Mb, NTlb).

n2 (T2, МЗ, ТЗ))

218 Часть I. Язык Prolog

А)

Б)

 

м>х

ins{T1,X,NT1)

=>

м>х sfTI.X.NTIa.Mb.NTIb)

£к'

М2>Х

ins[T1,X, NTIa, Mb,NT1b)

Рис, 10.5. Некоторые варианты использования отношения ins: a) ins (п2 <Т1, Я, Т2), X, г.2 (NT1, М, T2));6)ins(п2 {71, М, Т2), X, пЗ (NTIa, Mb, STlb, N„ T2)l;

в) ins i пЗ (Tl,M2, Т2, Ю, ТЗ}, X, n.2 (NTIa,Mb, NTlbj,M2, п2 (Т2, №. ТЗ)}

В листинге 10.1 приведена полная программа вставки в двоично-троичный сло­варь, а в листинге 10,2 приведена программа отображения двоично-троичных деревьев.

Листинг 10.1. Программа вставки в двоично-троичный словарь; в этой программе попытки вставки дублирующегося элемента завершаются неудачей

% Вставка в деоичко-тсоичный слозаоь

add23[ Tree, X, Treel):-ins{ Tree, X_r Treel).

add23(Tree, X, n2 { Tl, MZ, T2}) ins(Tree, X_r Tl, M2, T2)..

del23i Tree, X, Treel):-add23(Treel, X, Tree).

4 Ввести X в дерево Tree, получив дерево Treel % Дерево растет в ширину

:- % Дерево растет в высоту Удалить X из дерева Tree, получив дерево Treel

ins(nil, х, ЦУ.)).

ins (1[А), X, 1(A), X, 1(Х)):-gt (X, А).

ins (1(A), X, 1(Х),А, 1(A)):-gt(A, X).

-

Т2}, х, п2 (ЫТ1, И» Т2))

ms(n2{ T1, gt(М, X), ins(Tl, X, NTl).

Mb, NTlb, M, T2))

ins! n2[ Tl, M, T2), X, пЗ (MTI gt; М, x),

ins (Tl, X, NTla, Mb, NTlb).

ins [ n2 (Tl, M, T2), X, n2 [ Tl, M, BT2]):-

gt{ x, M),

ins(T2, X, KT2). last n2 [ Tl, M_r T2), S, n3 [ Tl, M, MT2a, Mb, NT2b)) gt(X, M),

Глава 10. Усовершенствованные методы представления деревьев

ins I T2, X, HT2a, Mb, NT2b),

ins (n3 (Tl, M2, T2, M3, ГЗ), X, Г.ЗС NTl, M2, T2, M3, T3}):-gt (И2, X),

ins [ Tl, x, NTl).

ins(n3(Tl, M2, T2, КЗ, T3), X, n2< ETla, Mb, NT lb), K2, nZ{ T2, M3, T3)l:-gt{ M2, x), ins(Tl, X, HTla, Kb, NTlb).

ins(n3 (Tl, M2, T2, КЗ, ТЗЬ X, n3 [ Tl, M2, NT2, МЗ, ТЗ)):-gt(x, M2), gt (МЗ, х), ins(T2, X, NT2).

insl пЗ (Т1, М2, T2_r МЗ, ТЗ), X, п2 (Т1, N2, ЫТ2а), Mb, r\2 £ НТ2Ь, МЗ, ТЗ}):-gtl X, М2), gt (МЗ, X), "inst T2, X, NT2a_f Mb, NT2b).

ins[ n3(Tl, M2, T2, МЗ, ТЗ), X, п3 1 Т1, Н2, Т2, МЗ, NT3)):-gt(X, МЗ), ins(тз, х, NT3).

ins[ пЗ (Т1, М2, Т2, МЗ, ТЗ), X, п2(Т1, М2, Т2), МЗ, n2(NT3a, Mb, NT3b) >:-

gt (;•:, мз),

ins! ТЗ, X, НТЗа, Mb', NT3b).

Листинг 10.2.Программа отображения двоично-троичного словаря (слева) и словарь, который приведен на рис. 10 .2, отображенный с помощью этой программы (справа) ■ Отображение двоично-троичного словаря _____________________________________________________ show { Т}:-show[T, 0),

J

shOTa

nil,

show(1 (ft),H):-

tab[H), write (ft), nl.

T-

show(n2[Tl,M,T2), H) HI is H+b, show(T2, Hi), tab(H), write(--j, nl, tab[H), write(M), nl, tab[K), write (—), nl, shcw(Tl, Hi).

 

show С n3{ Tl, M2, T2	КЗ
Hi is H+5,
show(T3, Hi)r
tab(H), write!-->,	nl,
tab(H), write(M3),	nl,
show(T2, Hi) r
tab{H), write(M2),'	nl,
tab(H), write(—),	nl,
show(Tl, Hi).

T3), H)

-

 

	--
		12 10	12 10
			1
		4 3	4 3 1

 

Часть I. Язык Prolog

В данной программе иногда происходит ненужный перебор с возвратами. Напри­мер, если выполнение отношения ins с гремя параметрами завершается неудачей, то вызывается отношение ins с пятью параметрами и при этом отменяется часть вы­полненной работы. Эту причину снижения эффективности можно легко устранить, например, переопределив отношение ins следующим образом: ins2; Tree, X, HewTrees)

где NewTrees - список, имеющий длину 1 или 3, который соответствует таким ус­ловиям: HewTrees = [ UewTree], если ins{ Tree, X, NewTree)

HewTrees = [ ЯТа, Mb, NTb], если ins (Tree, X, ЫТа, Mb, NTb)

В связи с этим отношение add.23 должно быть переопределено таким образом:

add23C T, X, 11):-ias2! Т, X, Trees), combine(Trees, TlJ.

Отношение combine должно формировать одно дерево, 71, из списка Trees.

Упражнения

10.1. Определите отношение
in! Item, Tree)

для поиска элемента Item в двоично-троичном словаре Tree.

10.2. Откорректируйте программу, приведенную в листинге 10.1, для предотвраще­
ния перебора с возвратами (определите отношения ins2 и combine).