Поиск в глубину и итеративное углубление

При использовании формулировки задачи в виде пространства состояний может быть предусмотрено много подходов к поиску пути решения. Двумя основными стра­тегиями поиска являются поиск в глубину и поиск в ширину. В этом разделе рас­сматриваются стратегия поиска в глубину и ее вариант, называемый итеративным углублением.

Начнем разработку данного алгоритма и его вариантов с анализа описанной ниже простой идеи.

Чтобы найти путь решения Sol от заданного узла Ы до некоторого целевого уз­ла, необходимо реализовать в программе следующие операции:

• еслив - целевой узел, то Sol = [N];

• иначе, если существует узел-преемник N1 узлам, такой, что имеется путь Soil от узла N1 до целевого узла, то Sol = [ N | Soil].

Эта формулировка может быть переведена на язык Prolog следующим образом:

solve С N, т):-goal С И).

solve С К, [ К | Soil]):-S< Ы, N1), solve! Ml, Soil).

По сути, эта программа представляет собой реализацию стратегии поиска в глу­бину. Ее называют поиском в глубину с учетом того, в каком порядке рассматрива­ются варианты в пространстве состояний. Каждый раз, когда программе поиска в глубину предоставляется возможность продолжить поиск путем перехода к одному из нескольких узлов, она всегда предпочитает выбрать из них самый глубокий. Са

Часть II. Применение языка Prolog в области искусственного интеллекта

мым глубоким узлом является тот, который расположен дальше всех от начального узла. На рис. 11.4 показано, в каком порядке посещаются узлы. Этот порядок соот­ветствует трассировке выполнения программы Prolog при поиске ответа на следую­щий вопрос:

7- solve (a, Sol).

 

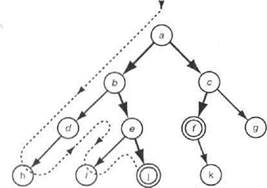
Рис. 11.4. Простое пространство состояний: a — начальный узел, f иj — целевые узлы. По-

рядок. в котором программа, реализующая стратегию поиска я глубину, посещает узлы в этом пространстве состояний, будет следую­щим: а. Ь, d, А, e, i, j. Найденным решением яв­ляется [а,Ь,е,]При переборе с возвратами обнаруживается еще одно решение — 1й,с,£]

Поиск в глубину в наибольшей степени приемлем для рекурсивного стиля про­граммирования на языке Prolog. Причина этого состоит в том, что сама система Prolog при выполнении цели проверяет варианты по принципу поиска в глубину.

Стратегия поиска в глубину является простой и удобной для программной реали­зации и может успешно применяться в определенных случаях. Программы решения задачи с восемью ферзями (см. главу 4), по сути, были примерами поиска в глубину. Формулировка задачи с восемью ферзями на основе пространства состояний, которая может использоваться в приведенной выше процедуре solve, состоит в следующем.

• Узлами являются позиции на доске, в которых на подряд идущих вертикаль­ных рядах доски помещено от нуля или больше ферзей.

• Узел-преемник формируется путем помещения еще одного ферзя на следую­щий вертикальный ряд доски таким образом, чтобы он не нападал ни на одно­го из имеющихся ферзей.

 

• Начальным узлом является пустая доска, представленная пустым списком.

• Целевым узлом является любая позиция с восемью ферзями {правило выбора преемника гарантирует, что ни один ферзь не нападает на другого).

Если позиция на доске представлена как список координат Y ферзей, то эту фор­
мулировку можно представить в виде программы следующим образом:
s{ Queens, [Queen Queens]):-
member! Queen, [1,2,3,4,5,6,7,8]!, \ Поместить ферзя Queen на любой

% горизонтальный ряд

noattacki Queen, Queens).

goal (l_i_i _>_<_, _,_>_}) -_____________________________ Позиция с 8 ферзями________________

Глава 11. Основные стратегии решения проблем

Отношение noattack требует, чтобы ферзь Queen не нападал ни на одного из ферзей в списке Queens; это отношение можно легко представить в программе, как показано в главе 4. Вопрос?- solvet (], Solution).

будет вырабатывать список позиций на доске со пес возрастающим количеством фер­зей. В конечном итоге в этом списке будет представлена безопасная конфигурация с восемью ферзями. Такой вопрос позволяет также найти альтернативные решения с помощью перебора с возвратами.

Стратегия поиска в глубину часто успешно реализуется, как и а этом примере, но имеется также много ситуаций, при которых рассматриваемая простая процедура solve может столкнуться с затруднениями. Действительно ли это произойдет или нет, зависит от пространства состояний. Для того чтобы нарушить работу процедуры solve при решении задачи, представленной на рис. 11.4, достаточно внести неболь­шое изменение в формулировку этой задачи: добавить дугу от h до d, создав тем са­мым цикл (рис. 11.5). В таком случае поиск будет осуществляться следующим обра­зом: программа начнет работу с узла а и спустится к h, следуя по крайней левой вет­ви графа. В этот момент, в отличие от рис. 11.4, узел h имеет преемника, d. Поэтому в процессе выполнения программы происходит не возврат из узла и, а переход к узлу d. Затем будет найден преемник d, узел h и т.д., в результате чего программа начнет переходить по циклу от d к ], и наоборот.

Очевидным усовершенствованием программы поиска в глубину является введение механизма распознавания цикла. В соответствии с ним любой узел, который уже встречался в пути от начального узла к текущему узлу, больше не должен рассмат­риваться. Это условие можно сформулировать с помощью следующего отношения: depthfirst! Path, Node, Solution)

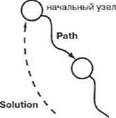
Как показано на рис. 11.6, Mode — это состояние, из которого необходимо найти путь к целевому состоянию, Path — это путь (список узлов) между начальным узлом и узлом Node, Solution - это путь Path, проходящий через Node к целевому узлу.

Для упрощения программирования пути в рассматриваемой программе представ­лены в виде списков с узлами в обратном порядке. Параметр Path может использо­ваться для двух назначений.

1. Для исключения вероятности того, чтобы в программе рассматривались пре­емники узла Mode, которые встречались ранее (распознавание циклов).

2. Для формирования пути решения Solution.

 

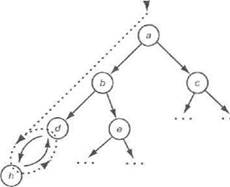
Рис. 11.5- Начиная с узла а, процесс поиска в глубину оканчивается возникновением цикла между узлами d и h следующим обра-

зом: а, Ь, a, h, d, ft, d,

234 Часть II. Применение языка Prolog в области искусственного интеллекта

Node

 

 

*--0