Поиск пути

Предположим, что G - граф, а К и Z - два узла в графе G. Определим следующее отношение: path (A, Z, G, Р}

где Р - ациклический путь между узлами А и Z в графе G. Путь Р представлен как список узлов в этом пути. Если С- - граф, показанный на рис. 9.11, а, то имеют ме­сто следующие варианты пути:

path(a, d, G, [a,b,d] } path (a, d, G, [a,b,c,d])

Поскольку путь не должен содержать циклов, то любой узел может входить в со­став пути не больше одного раза. Ниже описан один из методов поиска пути.

Чтобы найти ациклический путь Р между узлами А и Z в графе G, необходимо выполнить следующие действия:

1. если А = Z, то Р = [А];

2. в противном случае найти ациклический путь PI от некоторого узла Y до Z, а затем найти пути от А до Y, избегая узлов, которые входят в путь Р1.

Эта формулировка указывает на то, что требуется еще одно отношение для поиска пути с учетом ограничения, согласно которому необходимо избегать использования некоторого подмножества узлов (обозначенного выше как?1). Поэтому определим еще одну процедуру следующим образом: pathl (A, Pathl, G, Path)

Как показано на рис. 9.12, эта процедура имеет следующие параметры.

• А — узел.

• G - граф.

• Pathl - путь в графе G.

• Path - ациклический путь в графе G, который проходит от А до начала Pathl и продолжается вдоль Pathl вплоть до его конца.

Отношения path и pathl связаны между собой следующим отношением:

path( A, Z, G, Path):- pathl! ft, [Z], G, Path),

Глава 9, Операции со структурами данных

Pith I

 

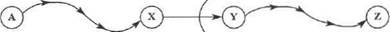
Path

Рис. 9.12. Отношение pa thl,где Path - путь от, а до Z; последний уча­сток пути Path совпадает с Pathl

Схема, приведенная на рис. 9.12, показывает, что отношение pathl может быть определено рекурсивно. Как граничный случай может рассматриваться ситуация, при которой начальный узел пути Pathl (узел Y на рис. 9.12) совпадает с начальным узлом пути Path (узлом А). Если же начальные узлы не совпадают, то должен быть узел X, такой, что:

1. Y является смежным по отношению к X; и

2. X не входит в состав пути Pathl; и

3. fat.-, должен соответствовать отношению pathl (А, [X | Pathl], G, Path).

Окончательный вариант программы показан в листинге 9.8. В этой программе от­ношение member представляет собой отношение проверки принадлежности к списку. Отношение adjacent* X Y, G)

означает, что в графе G существует дуга от X до Y. Определение этого отношения за­висит от представления графа. Если G представлен в виде пары множеств (узлов и ребер) следующим образом: G = graph (Nodes, Edges) то должен применяться следующий вариант этого отношения:

adjacent [ х, Y, gracb(Nodes, Edges)):-member! е(хД), Edges)

member (e(Y,X), Edges). ЛИСТИНГ 9.8. ПОИСК ациклического пути P a t h ОТ АДО Z В Графе Graph

"Г path ("A,"Т_г".... Graph, Path™^

path(Д, в, Graph, Path):-pathl [ A, [Z], Graph, Path].

pathl! A, [A | Pathl], _, [A | Pathl]).

pathl (A, [Y | Pathl], Graph, Path):-adjacent (X, Y, Graph),

not member {X, Pathl)_r % Условие, исключающее образование цикла

pathl С A, [X, Y ] Pathl], Graph, Path).

Классической задачей теории графов является поиск гамилътопоеа пути; так на­зывается ациклический путь, который охватывает все узлы в графе. Используя от­ношение path, эту операцию можно выполнить следующим образом;

bamiitor.ian_ Graph, Path):-path!,, Graph, path), covers_ Path, Graph).

covers; Path, Graph):-

not { node! к, Graph), not member! н, Path)). где node (N, Graph) означает, что N - узел в графе Graph.

Часть I. Язык Prolog

Путям могут быть поставлены в соответствие стоимости. Стоимость пути пред­ставляет собой сумму стоимостей дуг в этом пути. Если дугам не назначены стоимо­сти, то можно вести речь не о стоимости, а о длине пути, считая, что каждая дуга в пути имеет стоимость, равную 1, Отношения path и pat hi можно модифицировать таким образом, чтобы в них учитывалась стоимость, введя дополнительный пара­метр, стоимость, для каждого пути следующим образом:

path С A, Z, Б, Р, С) pathl[ ft, PI, C1, G, p, c)

где С — стоимость пути Р и С1 стоимость пути Р1. В таком случае отношение adjacent также должно иметь дополнительный параметр — стоимость дуги. В лис­тинге 9.9 приведена программа поиска пути, которая вычисляет путь и его стои­мость.

Листинг 9.9. Поиск пути в графе; P a t h - это ациклический путь со стоимостью Cost от А до z в графе Graph

Г^,path('"А"^2™Gra™p'Г,""Path,'Cost")':""'

% Path - ациклический путь со стоимостью Cost от А до Z в графе Graph

path( A, Z, Graph, Path, Cost):-pathl (A, [Z], 0, Graph, Path, Cost).

pathlf A, [A! Pathl], Costl, Graph, [A | Pathl], Costl).

pathl r A, v Pathl], Costl, Graph, Path, Cost}:-adjacent< X, Y, CostXY, Graph), not member! X, Pathl), Cost2 is Costl + CostXY, pathl< A, [X, Y | Pathl], Costs, Graph, Path, cost).

Эта процедура может также использоваться для поиска пути с минимальной стоимостью. Такой путь между двумя узлами (nodel и node2) можно найти в неко­тором графе Graph с помощью следующих целей: path! nodel, node2. Graph, MinPath, MinCest), not (path{ nodel, node2, Graph,, Cost), Cost < Mincost)

Кроме того, можно найти путь с максимальной стоимостью между любой парой узлов в графе Graph с помощью следующих целей: path! _, _, Graph, MaxPath, MaxCoatb not (path; _, _, Graph, _, Cost!, Cost > MaxCost)

Необходимо отмстить, что это — весьма неэффективный метод поиска пути с ми­нимальной или максимальной стоимостью. В нем случайным образом исследуются все возможные пути, поэтому он полностью непригоден для больших графов, по­скольку требует значительных затрат времени. Задача поиска пути часто возникает в проблематике искусственного интеллекта. Более приемлемые методы поиска опти­мальных путей будут рассматриваться в главах 11 и 12.