, , , , .
, . , , . ? 99% . , , .
( ), . , , , , , . , , .
, ( , ). .
:
a) , ;
b) .
:
a) ;
b) if, , (while, for), .
(DU )
DU DU . . DU .
DU :
1. ( ).
2. . :
a) ( ) ;
b) ( ) ( ).
3. DU .
3. :
3. :
3. :
DU 
, x , i x, j x.
4. ( DU ).
5. .
6. .
. .
|
|
|
, , (Insertion Sort), . :
: n < 
>.
: ( ) < 
> , 
, :
0 // ()
1 for j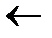 
2 to length[ A ]
2 do key 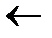A [ j ]
3 i 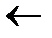j 1
4 while i > 0 A [ i ] > key
5 do A [ i + 1] 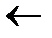A [ i ]
6 i 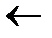i 1
7 A [ i + 1] 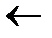key
8 end for
1. ( 2).
2
2. ( 3).
3
3. :
DEF(0)={A}
DEF(1)={j}
DEF(2)={key}
DEF(2)={i}
DEF(5)={A}
DEF(6)={i}
DEF(7)={A}
3. :
USE(1)={A}
USE(2)={j}
USE(3)={i}
USE(4)={A, key, i}
USE(5)={A,i}
USE(6)={i}
USE(7)={i, key}
3. :
DU: {[A,0,1]; [A,0,4]; [A,0,5];
[j,1,2];
[key,2,4]; [key,2,7];
[i,2,3]; [i,2,4]; [i,2,5]; [i,2,6]; [i,6,7];[i,6,3];[i,6,4];[i,6,5]}
4. ( DU ). (), (). 4 - 9 .
| A |
| A |
4 [A, 0, 1] [A, 0, 4]
| key |
| j |
| A |
5 [A, 0, 5], [j, 1, 2] [key, 2, 4]
| key |
| i |
6 [key, 2, 7] [i, 2, 3]
| i |
| i |
7 [i, 2, 4] [i, 2, 6]
| i |
| i |
8 [i, 6, 7] [i, 2, 5]
| i |
| i |
| i |
9 [i, 6, 3], [i, 6, 4] [i, 6, 4]
|
|
|
5. .
1: 0-1-2-3-4-5-6-7-8 // N > 1,
2: 0-1-2-3-7-8 // N > 1,
3: 0-1-2-3-4-7-8 // N > 1,
4: 0-1-2-3-4-5-6-3-4-5-6-7-8 // N > 1,
6. :
1: : N = 6, A = {2, 5, 4, 6, 1, 3} , .
: A = {1, 2, 3, 4, 5, 6}.
2: : N = 6, A = {2, 4, 5, 6, 1, 3} .
: A = {1, 2, 3, 4, 5, 6}.
3: : N = 6, A = {1, 2, 3, 4, 5, 6} .
: A = {1, 2, 3, 4, 5, 6}.
4: : N = 6, A = {1, 2, 4, 5, 6, 3} .
: A = {1, 2, 3, 4, 5, 6}.
