Базовые понятия
Различают три типа условий:
a) простое условие:
1) булева переменная;
2) выражение отношения (арифметическое выражение)
Вид:
,
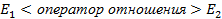где 
b) составное условие. Оно содержит в себе несколько простых условий и включает:
1) простые условия;
2) булевы операторы (OR, AND, NOT);
3) пара скобок.
в) булево выражение, не содержащее в себе арифметических выражений.
Существуют методики тестирования условий – это методика тестирования ветвей и методика тестирования области определения.
Тестирование ветвей – это простейшая методика, позволяющая проверять простые условия и ветви TRUE / FALSE. Вторая методика – методика тестирования области определения – тестирует выражения отношения. Составляются следующие тесты для логических выражений:
;
;
.
Тестирование условий имеет следующие достоинства:
a) достаточно простое выполнение измерения тестового покрытия условия;
b) тестовое покрытие условий в программе является фундаментом для генерации дополнительных тестов программы;
c) данная методика эффективна не только для обнаружения ошибок в условиях, но также и для обнаружения других ошибок в программе.
Методика тестирования ветвей и операторов отношений была разработана в 1989 году. Она применима при выполнении следующих ограничений:
a) все булевы переменные и операторы отношения входят в условие только по одному разу;
b) в условии отсутствуют общие переменные.
Ограничение на результат фиксирует возможные значения аргумента простого условия, если он один, или соотношение между значениями аргументов, если их несколько. Ограничение составного условия обозначается следующим образом:
,
где n – количество простых условий в составном условии.
Если, к примеру, 
– булевы переменные, то 
. Если – выражение отношения, то 
.
На основе ограничения составного условия (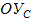
) строится ограничивающее множество ОМ. Элементами ограничивающего множества являются сочетания всех возможных значений. Построение ОМ выполняется путем подстановки в константные формулы ОМ& или OMOR. Например:
для условия типа И (а & b)
ОМ& = {(false, true), (true, false), (true, true)};
для условия типа ИЛИ (а от b)
ОМor = {(false, false), (false, true), (true, false)}.
