Если отказаться полностью от тестирования всех путей, то можно показать, что критерием покрытия является выполнение каждого оператора программы, по крайней мере, один раз. Это метод покрытия операторов отношений. К сожалению, это слабый критерий, так как выполнение каждого оператора, по крайней мере, один раз есть необходимое, но недостаточное условие для приемлемого тестирования по принципу белого ящика.
Метод тестирования ветвей и операторов отношений выполняется по следующему алгоритму:
a) построение множества ограничений условий;
b) выявление ограничения результата по каждому простому условию;
c) построение ограничивающего множества, посредством подстановки значений в константные формулы;
d) для каждого элемента ограничивающего множества разрабатываются тестовые варианты.
Тестирование этим методом будет также рассмотрено на примере процедуры сортировки вставкой. В данной процедуре имеет место составное условие (строка 4 листинга процедуры).
Insertion_Sort(A)
1 for j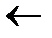 
1 to length[ A ]
2 do key 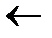A [ j ]
3 i 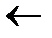j – 1
4 while i > 0 и A [ i ] > key
5 do A [ i + 1] 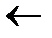A [ i ]
6 i i – 1
7 A [ i + 1] key
8 end for
Таким образом, имеется выражение (i > 0) & (A [ i ] > key). Это выражение является составным и содержит в себе два простых выражения.
Множество ограничения составного условий: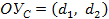 
, где 
Ограничение на результат: 
.
Константная формула:
,
где 
(i > 0),
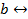(A [ i ] > key).
Таблица значений формулы для построения ограничивающего множества (таблица 1):
Таблица 1 – Значения переменных для отношения выражения
| 
| 
|
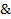
Ограничивающее множество: 
.
Построение тестовых вариантов:
ТВ 1: Исходные данные: N = 5, A = {3, 2, 8, 9, 1} – проверка остановки сдвижки.
Ожидаемый результат: A = {3, 2, 8, 9, 1}.
ТВ 2: Исходные данные: N = 9, A = {9, 8, 17, 298, 1, 1, 4, 2, 4} – проверка на то, нарушает ли текущий элемент (key) порядок в массиве размером от 2 до N элементов.
Ожидаемый результат: A = {1, 1, 2, 4, 4, 8, 9, 17, 298}.
ТВ 3: Исходные данные: N = 3, A = {10, 2, 8} – проверка процесса сортировки.
Ожидаемый результат: A = {2, 8, 10}.
