Рассмотрим теплопередачу между двумя жидкостями через разделяющую из многослойную плоскую стенку. Здесь передача теплоты делится на три процесса:
1) В начале теплота передается от горячего теплоносителя tж1 к поверхности стенки путем конвективного теплообмена, который может сопровождаться излучением. Интенсивность процесса теплоотдачи характеризуется коэффициентом теплоотдачи a1.





















2) Затем теплота
теплопроводностью переносится поочередно от одной поверхности стенки к другой, которая характеризуется коэффициентом теплопроводности l(l
1,…,l
n).
| Рисунок 10.1 - Распределение температур при теплопередаче через многослойную плоскую стенку
| |
3) И, наконец, теплота опять путем конвективного теплообмена передается от поверхности стенки к холодной жидкости t
ж2. Этот процесс характеризуется коэффициентом теплоотдачи a
2.
При стационарном режиме плотность теплового потока во всех трех процессах одинакова и может быть записана следующим образом:
1. по закону Ньютона - Рихмана
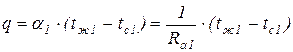 ,
,
2. по закону Фурье
 ,
,
3. по закону Ньютона - Рихмана
 ,
,
где  и
и  - термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю.
- термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю.
Из вышеприведенных уравнений составив систему уравнений:
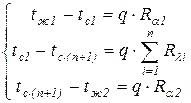 ,
,
и сложив правые и левые части, получим уравнения теплопередачи через многослойную плоскую стенку:
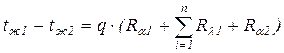
или
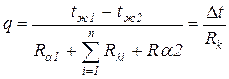 ,
,
где  - температурный напор, заданный условиями задачи;
- температурный напор, заданный условиями задачи;
Rk - термическое сопротивление теплопередачи от горячего теплоносителя к холодному.
Величина, обратная Rk, называется коэффициентом теплопередачи К:
 ,
,
Коэффициент теплопередачи К характеризует интенсивность процесса теплопередачи от горячего теплоносителя к холодному через разделяющую их стенку.
Тогда уравнение теплопередачи можно записать:
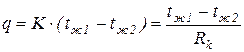 или
или 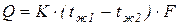
Граничные температуры определяются из (3.4):
 ,
,
Очевидно, что для однослойной плоской стенки формулы справедливы, где  ,
,  , tc(n+1)=tc2.
, tc(n+1)=tc2.





















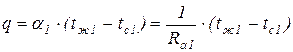 ,
, ,
, ,
, и
и  - термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю.
- термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю.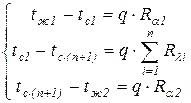 ,
,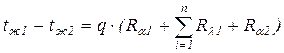
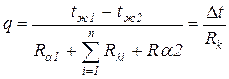 ,
, - температурный напор, заданный условиями задачи;
- температурный напор, заданный условиями задачи; ,
,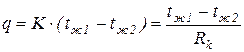 или
или 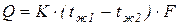
 ,
, ,
,  , tc(n+1)=tc2.
, tc(n+1)=tc2.



