Точка участвует в двух движениях одновременно (по оси X и по оси У). Значения координат X и У колеблющейся точки одновременно повторяются через одинаковые промежутки времени Т, равные наименьшему общему кратному периодов колебаний вдоль осей ОХ и ОУ:
Поэтому траектория точки - замкнутая кривая, форма которой зависит от соотношения частот, амплитуд и начальных фаз складываемых колебаний. Эти кривые называются фигурами Лиссажу.
Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат X и У и расположены по обе стороны от них на расстояниях, соответственно равных А и В (рис.6 и 7). Отношение частот 
и 
складываемых колебаний равно отношению количества пересечений фигуры Лиссажу с прямой, параллельной оси У, к количеству пересечений с прямой, параллельной оси X.
Рис.6.
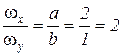
Рис.7.
