1) и 2) в тексте лекции.
3) Пользуясь первым свойством, вычислить первые 15 чисел Фибоначчи.
4) Пользуясь вторым свойством, вычислить любое число Фибоначчи не меньше 25-го.
5) Проверьте на практике свойства чисел ряда Фибоначчи 4-9. Приведите примеры. Доказательств приводить не надо.
К этому уроку можно выполнить курсовую работу на тему:
"Доказать 3 любых свойства (2-11) чисел ряда Фибоначчи"
Чи́сла Фибона́ччи — последовательность целых чисел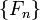 
, заданная с помощью рекуррентногосоотношения
.
Последовательность чисел Фибоначчи начинается так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 … (Шаблон:OEIS)
Иногда числа Фибоначчи рассматривают и для неположительных номеров n. Ряд, соответствующий определению чисел Фибоначчи 
: …, −55, 34, −21, 13, −8, 5, −3, 2, −1, 1, 0, 1, 1, 2, …
<tr><th> 
</td><td>-55</td><td>34</td><td>-21</td><td>13</td><td>-8</td><td>5</td><td>-3</td><td>2</td><td>-1</td><td>1</td><td>0</td><td>1</td><td>1</td><td>2</td><td>3</td><td>5</td><td>8</td><td>13</td><td>21</td><td>34</td><td>55</td></tr> </table> Легко видеть, что 
. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств (но не все!).
| n</td><td>-10</td><td>-9</td><td>-8</td><td>-7</td><td>-6</td><td>-5</td><td>-4</td><td>-3</td><td>-2</td><td>-1</td><td>0</td><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td><td>6</td><td>7</td><td>8</td><td>9</td><td>10</td> |
| Содержание [показать] |
Формула Бине 
Править
Формула Бине выражает в явном виде значение как функцию от 
:
,
где 
— золотое сечение. При этом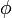 
и 
являются корнями квадратного уравнения 
.
Из формулы Бине следует, что для всех 
, есть ближайшее к 
целое число, то есть 
. В частности, справедлива асимптотика 
.
Тождества Править
§ 
§ 
§ 
§ 
§ 
§ 
§ 
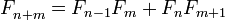
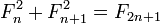
§ Числа Фибоначчи представляются значениями континуант на наборе единиц: 
, то есть
, а также 
,
где матрицы имеют размер 
, 
— мнимая единица.
§ Для любого n,
Эта формула даёт быстрый алгоритм вычисления чисел Фибоначчи.
§ Подсчёт определителей даёт
Свойства Править
§ Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. 
. Следствия:
§ 
делится на тогда и только тогда, когда 
делится на (за исключением 
). В частности, делится на 
(то есть является чётным) только для 
; делится на 
только для 
; делится на 
только для 
и т. д.
§ может быть простым только для простых (с единственным исключением 
) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример — 
. Неизвестно, бесконечное ли количество чисел Фибоначчи являющихся простыми.
§ Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, еёхарактеристический многочлен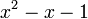 
имеет корн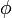и и 
.
§ Отношения 
являются подходящими дробями золотого сечения 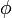и, в частности, 
.
§ Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
.
§ В 1964 J. H. E. Cohn доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: 
, 
, 
, 
. При этом для n=0,1,12 верно утверждение 
.
§ Производящей функцией последовательности чисел Фибоначчи является:
§ Множество чисел Фибоначчи совпадает с множеством положительных значений полинома
,
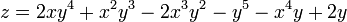на множестве неотрицательных целых чисел 
и 
(P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p.193).
§ Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
§ Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60. Если от каждого числа брать по две последние цифры, то они образуют последовательность с периодом, равным 300. Если брать по три последние цифры — с периодом 1500, по четыре — с периодом 15000, по пять — с периодом 150000, по шесть — с периодом 1500000.
