Обнаружено много интересных соотношений между числами ряда Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21,...
1) Принцип образования членов этого ряда приводит к следующему соотношению между любыми его тремя рядом стоящими членами Sn -2, Sn -1 и Sn:
Sn = Sn -1 + Sn -2.
Эта формула дает возможность по первым двум членам ряда установить его третий член, по второму и третьему - четвертый, по третьему и четвертому - пятый и т. д.
2) Интересно было бы уметь сразу получить любой член ряда Sn, зная лишь номер n его места. Оказывается, это вполне возможно, но здесь мы столкнемся с одной из удивительных неожиданностей, которые нередки в математике.
Любой член ряда Фибоначчи - число целое, номер места - тоже число целое. Естественно было бы ожидать, что любой член ряда Sn получается в зависимости от номера и занимаемого им места при помощи действий только над целыми числами (например, как в прогрессиях). Но это не так. Не только целые числа, но даже все целые и дробные (рациональные) бессильны образовать интересующую нас формулу.
Из затруднительного положения помогают выйти два иррациональных числа:
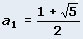 и
и 
Так вот, если n - номер места, то любой член Sn ряда Фибоначчи вы можете получить по формуле:
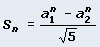
3) Зная, как любой член Sn ряда Фибоначчи определяется по номеру n занимаемого им места:
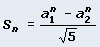 , где
, где 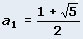 и
и 
легко доказать, что любая пара соседних чисел ряда Фибоначчи Sn и Sn+1 удовлетворяет одному из уравнений x 2- xy-y 2=±1, причем, если y=Sn, то x=Sn +1.
4) Очень забавный вид у формулы для суммы n членов ряда Фибоначчи:
S 1 + S 2 +... + Sn = Sn +2 - 1
Сумма n первых членов ряда Фибоначчи на 1 меньше (n +2) -го члена того же ряда.
5) Сумма квадратов чисел ряда Фибоначчи выражается через произведение двух соседних членов того же ряда:
S 12 + S 22 +... + Sn 2 = Sn · Sn +1
Доказательство этого свойства - тема для курсовой работы.
6) Квадрат каждого члена ряда Фибоначчи, уменьшенный на произведение предшествующего и последующего членов, дает попеременно то +1, то -1.
Sn 2 - Sn -1· Sn +1 = (-1) n +1.
7) S 1 + S 3 +... + S 2 n -1 = S 2 n .
8) S 2 + S 4 +... + S 2 n = S 2 n +1 - 1.
9) В ряду Фибоначчи каждое третье число - четное, каждое четвертое делится на 3, каждое пятое - на 5, каждое пятнадцатое - на 10.
10) Невозможно построить треугольник, сторонами которого являются числа ряда Фибоначчи.
11) Если взять любые 4 последовательных числа ряда Фибоначчи и рассматривать произведение крайних членов и удвоенное произведение средних - как длины катетов прямоугольного треугольника, то длиной его гипотенузы будет один из членов этого ряда:
(an· an +3)2 + (2 an +1· an +2)2 = a 22 n +3.
Устали? тогда все.






