Рассмотрим уравнение
.
Пусть требуется найти его корень на отрезке [1,2]. В качестве численного метода использовать метод простых итераций.
Приводим исходное уравнение к виду (2):
В соответствии с (4) получим выражения для метода простых итераций
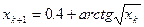
Ниже следует текст программы (script – файла):
e = 1e-04; %допустимая погрешность
xk = 1.5; %задаем значение первого приближения
I = 0; %счетчик итераций I устанавливаем в ноль
delta = xk;
while abs(delta) > e %начало цикла итераций
xk_plus_1 = 0.4 + atan(sqrt(xk)); %следующее приближение
delta = xk_plus_1 - xk; %текущая погрешность
xk = xk_plus_1; %перейти к следующему приближению
I = I+1;
end;
Str = ['Значение корня: ' num2str(xk) ];
disp(Str)
Str = ['Точность: ' num2str(delta) ];
disp(Str)
Str = ['Количество итераций: ' num2str(I) ];
disp(Str)
При заданном в качестве первого приближения значении 1.5 будут получены следующие результаты (требуемая точность установлена 10-4):
>> Значение корня: 1.2389
Точность: -5.971e-005
Количество итераций: 6
В заключение приведем пример программы численного решения этого же уравнения методом половинного деления (отрезок, содержащий корень определяется в программе). Отметим, что в качестве левой границы интервала сначала задается любое число на оси Х. Далее с некоторым шагом осуществляется смещение по этой оси вправо до тех пор, пока не будет найден отрезок, на котором функция меняет знак (факт изменения знака можно установить, перемножив значения функции в левой и правой границах интервала: если это произведение отрицательно, то функция меняет знак). Найденный отрезок и является исходным для поиска корня. Приведенный ниже текст программы реализует указанную логику действий:
e = 1e-04; %Устанавливаем допустимую погрешность
dx = 0.1; %шаг х при поиске интервала, содержащего корень
a = 1;
b = a;
while f(a)*f(b) > 0 %Определяем интервал, на котором
b = b + dx; % функция F(x) меняет знак
end;
a = b - dx;
x = (a+b)/2; % Первое приближение корня -
% середина найденного интервала
I = 1; % Счетчик итераций устанавливаем в "1"
X=[x]; % Формирование массивов для графиков
Y=[f(x)];
while abs(f(x)) > e
if f(x) * f(a) < 0 %Если функция имеет разные знаки
%на концах отрезка,
b = x; %сдвигаем правую границу
else
a = x; % иначе сдвигаем левую границу
end;
x = (a+b)/2; %и вычисляем следующее приближение
I = I + 1; %увеличиваем количество итераций на 1
X = [X x];
Y = [Y f(x)];
end;
Str = ['Значение корня: ' num2str(x) '; Количество итераций: ' num2str(I)];
disp(Str)
figure %Построение двух графиков в одном графическом окне
subplot(2, 1, 1);
plot(X, '-r'), grid on
subplot(2, 1, 2);
plot(Y, '-b'), grid on
В данном примере для корректной реализации необходимо создать еще один файл – файл-функцию, который имеет следующий вид:
function [ y ] = f (x)
y = 0.4 + atan(sqrt(x)) - x;
Имя функции «f», файл, в котором она находится, имеет имя «f.m», входным параметром является значение абсциссы «x», выходным – значение ординаты «y». Программа по ходу выполнения несколько раз обращается к функции, когда необходимо проверить знаки на концах интервала.
Результаты вычислений посредством метода половинного деления таковы:
>> Значение корня: 1.2389; Количество итераций: 9
Несмотря на несколько большее количество итераций, метод половинного деления является универсальным. Для его реализации нет необходимости вычислять производную (что особенно важно для сложных функций).
На следующих графиках проиллюстрирован процесс сходимости решения (верхний график – сходимость значения корня, нижний – сходимость значения функции к нулю).
Рассмотрим еще один пример решения уравнения, но методом Ньютона. Уравнение такое:
.
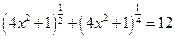Нетрудно видеть, что корни данного уравнения равны 
. Для реализации метода Ньютона необходимо записать функцию 
:
.
Производная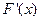 
имеет следующий вид:
Будем искать положительный корень уравнения. Поэтому в качестве первого приближения возьмем значение 1. Решить поставленную задачу можно посредством выполнения следующего файла сценария (script-файла):
% Решение уравнения методом Ньютона
% F(x)=0
% F(x)=(4x^2+1)^(1/2)+(4x^2+1)^(1/4)-12
% F'(x)=2x(2(4x^2+1)^(-1/2)+(4x^2+1)^(-3/4))
% Уравнение имеет два корня: sqrt(20) и -sqrt(20)
% В данном примере ищется положительный корень
% Первое приближение = 1
e = 1e-08; %допустимая погрешность
x_k = 1; %задаем значение первого приближения
I = 0; %счетчик итераций I устанавливаем в ноль
delta = x_k;
D = [ delta ];
while abs(delta) > e %начало цикла итераций
xk_plus_1 = x_k - fun(x_k) / fun1(x_k); %следующее приближение
delta = xk_plus_1 - x_k; %текущая погрешность
D = [ D delta ];
x_k = xk_plus_1; %переприсваиваем приближения, чтобы перейти к следующему
I = I+1;
end;
Str = ['Значение корня: ' num2str(x_k) ];
disp(Str)
Str = ['Точность: ' num2str(delta) ];
disp(Str)
Str = ['Количество итераций: ' num2str(I) ];
disp(Str)
plot(D)
Из текста видно, что для решения необходимы две функции: 
и 
(еще раз напомним, что имена файлов этих функций должны совпадать с именами самих функций). Указанные функции имеют вид:
function [ y ] = fun (x)
y = (4*x^2+1)^(1/2)+(4*x^2+1)^(1/4)-12;
и
function [ y1 ] = fun1(x)
y1 = 2*x*(2*(4*x^2+1)^(-1/2)+(4*x^2+1)^(-3/4));
Результат выполнения программы таков:
>> Значение корня: 4.4721
Точность: 1.7764e-015
Количество итераций: 4
На следующем графике представлено изменение текущей погрешности вычисления корня (видно, что погрешность быстро убывает и уже с третьего приближения практически равна нулю):
В заключение отметим, что в составе MatLab имеется функция fzero, позволяющая найти численно корень уравнения при условии, что задано его первое приближение. Для решения приведенного выше уравнения достаточно выполнить команду:
>> x0=1;
>> x=fzero('fun', x0)
и получить результат:
>> x =
4.4721
Параметры функции очевидны из примера. Если имеется файл функции (в данном случае fum.m), то при помощи команды fplot можно построить график функции (например, чтобы проиллюстрировать решение уравнения). Команда построения графика выглядит так:
>> fplot('fun', [-6 6]);
а результат ее показан на следующем рисунке:
Определенную трудность при численном решении уравнения представляет поиск первого приближения. Для упрощения процедуры поиска первого приближения можно использовать возможности Matlab по аналитическому исследованию функций (пакет расширения Symbolic Math).
В этом случае можно объявить символьную (аналитическую) переменную, аналитически описать на её основе функцию, представляющую правую часть уравнения, построить график этой функции и по графику визуально определить первое приближение корня. Далее, как и в предыдущем примере, организовать вычисления последовательных приближений корня уравнения.
Рассмотрим решение уравнения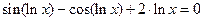 
. Производная правой функции части равна 
.
Следующий пример поясняет порядок решения указанной задачи. Отметим, что в тексте примера есть все необходимые комментарии, объясняющие смысл действий, производимых каждым оператором:
% решение трансцендентного уравнения методом Ньютона (методом касательных)
% с использованием аналитического представления функции F(x) и ее производной
syms x; % объявляется символьная (аналитическая) переменная
% определяется аналитическое описание функции F(x)
f = sin(log(x)) - cos(log(x)) + 2*log(x);
f1 = diff(f); % определяется производная функции F'(x)
% функция Matlab diff определяет производную (в данном случае – первую)
% по умолчанию функция Matlab diff определяет производную
% для определения второй производной и производных высших порядков
% в обращении к функции diff необходимо указать порядок производной,
% например, diff(f, 2) – для определения производной
ezplot(f), grid on, pause % строится график функции для визуального
% определения первого приближения корня.
% Функция pause используется для того, чтобы прервать выполнение программы
% для возможности визуальной фиксации приближенного значения корня и
% определения первого приближения по графику функции.
% Lля продолжения работы программы необходимо, не закрывая графического
% окна, нажать на клавишу Enter
x0 = input('Задайте значение x0: ') % вводом с клавиатуры
% задается первое приближение корня
% Функция input используется для организации диалога программы с
% пользователем по вводу первого приближения корня
err = 1e-05; % задается допустимая погрешность вычисления корня
delta = x0; % текущая погрешность вначале равна допустимой погрешности
X = [ x0 ]; % формируется вектор последовательных приближений
% корня к его конечному значению
n = 1; % номер первого приближения
N = [ n ]; % формируется вектор номеров приближений корня
% организуется цикл определения последовательных приближений корня
% методом Ньютона
while abs(delta) > err % повторять вычисления пока текущая погрешность
% больше допустимой
x1 = x0 - subs(f, x, x0) / subs(f1, x, x0); % Вычисляется следующее
% приближение корня.
% Функция SUBS используется для вычисления значения по аналитической формуле
% подстановкой в неё значения текущего приближения х0 вместо аналитической
% переменной х
delta = x1 - x0; % вычисляется текущая погрешность вычислений
x0 = x1; % следующее приближение становится текущим
X = [X x1]; % в вектор Х добавляется следующее приближение
n = n+1; % номер следующего приближения
N = [N n]; % в вектор N добавляется номер следующего приближения
end;
str_out = 'x = '; % формируется строка вывода результатов вычисления корня
res = num2str(x1);
str_out = strcat(str_out, ' ', res);
disp(str_out); % строка вывода отображается в командном окне
plot(N, X, 'Linewidth', 3, 'Color', [0 1 0]), grid on % строится график
% приближения корня
Следующие графики иллюстрируют результаты выполнения программы.
На первом рисунке представлен график функции, из которого видно, что значение корня лежит между значениями 1 и 2. Это дает возможность в качестве первого приближения взять, например, значение, равное 3, которое вводится с клавиатуры во время диалога.
На втором рисунке показано изменение приближенного значения корня в процессе последовательных итераций. Видно, что значение корня стабилизируется после восьмой итерации. Это значение корня равно 1.3749.
В данной работе необходимо в соответствии с заданием варианта написать программы вычисления корня уравнения в численном виде методом Ньютона, методом секущих, методом половинного деления, а также методом Ньютона с использованием аналитического представления функции. В тех случаях, когда уравнение решается численно (без аналитического представления функции) необходимо разработать функции Matlab для описания и 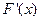. Во всех случаях построить графики, отражающие последовательные приближения корня к искомому значению (также приближенному, но с учетом заданной точности). Найденное значение корня необходимо сравнить со значением, вычисленным при помощи функции fzero.
В теоретической части работы, при ответе на контрольные вопросы в процессе занятия, необходимо знать существо каждого метода (идею, графическую интерпретацию, алгоритмы последовательных приближений значений корней).
