Метод простых итераций
В методе простых итераций приближения организуются по правилу:
xk+1= f(xk), где k = 0, 1, 2, 3,..., (4)
причем задается начальное (нулевое) приближение x0. При известном начальном приближении определяется первое приближение, затем второе, третье и т.д. до тех пор, пока не будет достигнута требуемая точность (т.е. разность между двумя последовательными приближениями не станет пренебрежимо малой).
Геометрическая интерпретация метода простых итераций представлена на рис.1 (для случая, если первое приближение лежит справа от истинного значения корня). Очевидно, что корнем уравнения является абсцисса точки пересечения двух графиков: y=x и y=f(x).
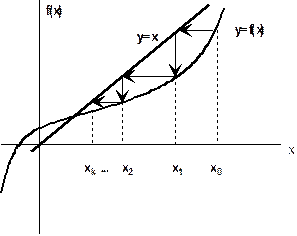
Рис.1.
Метод Ньютона
Алгоритм метода Ньютона строится исходя из представления функции F(x) в окрестности некоторой точки x* (предполагаемого корня уравнения), принадлежащей отрезку [a, b], в следующем виде:
F(xk+1) = F(xk) + (xk+1 - xk)* F ¢(xk) (5)
Исходя из равенства F(x)=0 и в соответствии с (5) (k+1) -e приближение определяется по правилу:
 , k=0,1,2,... (6)
, k=0,1,2,... (6)
Метод Ньютона иначе называется методом касательных (рис.2), поскольку для того, чтобы найти (k+1) -e приближение надо через точку xk провести вертикальную прямую до пересечения с кривой F(x), затем провести касательную до пересечения с осью абсцисс (точка x k+1), из точки xk+1 - вновь вертикальную прямую до пересечения с F(x) и т.д.

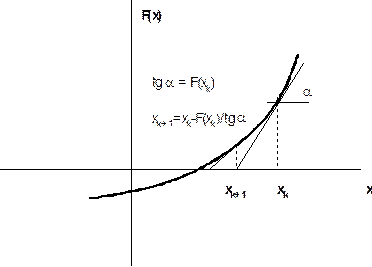
Рис.2
При программной реализации метода Ньютона приходится многократно вычислять первую производную функции F(x). Чтобы избежать этого, применяют модифицированный метод Ньютона, при котором производная вычисляется один раз в некоторой точке x*, принадлежащей отрезку [a, b]. Алгоритм модифицированного метода Ньютона реализуется при помощи следующего выражения:
 , где k = 0, 1, 2,... (7)
, где k = 0, 1, 2,... (7)
В разделе математики "Численные методы" доказывается, что если процесс, реализуемый по выражению (6) на отрезке [a, b] сходится, то и процесс, реализуемый по выражению (7), также сходится.






