ќпира€сь на основную теорему зацеплени€ можно спроектировать зубчатый механизм с самыми различными профил€ми зубьев.
ќднако практически выбор очертаний профилей ограничен требовани€ми, которые диктуютс€ соображени€ми кинематического, динамического, механического и эксплуатационного характера.
¬сем этим требовани€м в наилучшей степени удовлетвор€ет профиль, выполненный по эвольвенте круга.

Ёвольвентой называетс€ крива€, которую описывает люба€ точка пр€мой, кат€щеес€ без скольжени€ по окружности, получившей название основной.
L¬ -основна€ окружность.
√лавное свойство эвольвенты состоит в том, что нормаль в любой ее точке (ј, ¬, —...) касательно к основной окружности L¬, а, следовательно, основна€ окружность есть геометрическое место центров кривизны эвольвенты.
–ассмотрим построение эвольвентных профилей зубьев колес внешнего зацеплени€.
»з центров ќ1 и ќ2 проводим начальные окружности радиусами r 1 и r 2.
“очка – - полюс зацеплени€.
 - касательна€ к начальным окружност€м в т. –.
- касательна€ к начальным окружност€м в т. –.
„ерез т. – проводим нормаль n-n под заданным углом a к касательной  (ѕо √ќ—“у угол a=200).
(ѕо √ќ—“у угол a=200).
n-n - образующа€ пр€ма€.
a - угол зацеплени€.
»з точек ќ1 и ќ2 опустим перпендикул€ры на образующую пр€мую n-n.

 - радиус основной окружности 1 го колеса.
- радиус основной окружности 1 го колеса.

 - -//-//-//-//- 2 го колеса.
- -//-//-//-//- 2 го колеса.
ѕроводим основные окружности  и
и 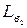 .
.

ƒл€ того, чтобы получить эвольвентные профили, надо образующую пр€мую n-n последовательно обкатить без скольжени€ по каждой из основных окружностей.
—начала дадим качение пр€мой n-n по основной окружности радиуса.
ƒл€ этого разделим отрезок –ј на несколько равных отрезков (например, на 4 отрезка) и отложим на основной окружности дуги, равные этим отрезкам.
¬ точках делени€ проведем касательные к основной окружности, отложив на них соответствующее число отрезков.
—оединив конечные точки лучей касательных плавной кривой, получим эвольвенту Ё 1, описывающую профиль зуба колеса 1.
јналогично построим и эвольвенту Ё 2 - профиль зуба колеса 2, перекатыва€ пр€мую n-n без скольжени€ по окружности радиуса.
ѕр€ма€ n-n €вл€етс€ общей нормалью к сопр€женным профил€м зубьев и называетс€ линией зацеплени€, т.к. только на этой линии происходит касание сопр€женных профилей.
ƒругими словами: лини€ зацеплени€ n-n представл€ет собой геометрическое место точек касани€ сопр€женных профилей при вращении колес.
Ёвольвентное зацепление полностью соответствует основной теореме зацеплени€, т.к. полюс зацеплени€ – будет всегда находитьс€ в одном и том же месте на линии центров ќ1ќ2 и передаточное отношение
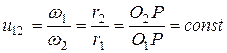
“.о. эвольвентное зацепление обеспечивает посто€нство передаточного отношени€.
»з  :
:  откуда
откуда 
»з  :
:  откуда
откуда 
“еперь получим 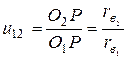
 «аключаем, что передаточное отношение не зависит от угла зацеплени€ a, а зависит только от радиусов основных окружностей.
«аключаем, что передаточное отношение не зависит от угла зацеплени€ a, а зависит только от радиусов основных окружностей.
Ёто имеет большое практическое значение.






