ѕределы и непрерывность
ќпределение. ≈сли по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число an, то говор€т, что задана числова€ последовательность { an }:
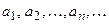 .
.
ƒругими словами, числова€ последовательность Ц это функци€ натурального аргумента: 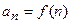 .
.
„исла 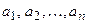 называютс€ членами последовательности, а число an Ц общим членом данной последовательности.
называютс€ членами последовательности, а число an Ц общим членом данной последовательности.
ѕримеры: 2,4,6,8,Е,2n,Е- монотонна€, неограниченна€.
1,0,1,0,Е - немонотонна€, ограниченна€.
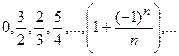 - немонотонна€, ограниченна€. –ассмотрим эту последовательность подробнее. »зобразим ее члены точками числовой оси.
- немонотонна€, ограниченна€. –ассмотрим эту последовательность подробнее. »зобразим ее члены точками числовой оси.
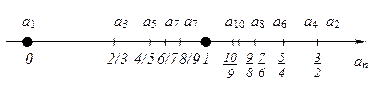
ћожно заметить, что члены последовательности с ростом n сколь угодно близко приближаютс€ к 1. ѕри этом абсолютна€ величина разности 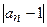 становитс€ все меньше и меньше:
становитс€ все меньше и меньше:
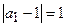 ,
, 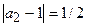 ,
, 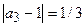 ,
, 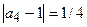 ,Е,
,Е, 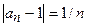 ,Е,
,Е,
то есть с ростом n величина 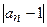 будет меньше любого сколь угодно малого положительного числа.
будет меньше любого сколь угодно малого положительного числа.
ќпределение. „исло ј называетс€ пределом числовой последовательности { an }, если дл€ любого сколь угодно малого положительного числа 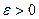 найдетс€ такой номер N (завис€щий от e), что дл€ всех членов последовательности с номерами n>N верно неравенство
найдетс€ такой номер N (завис€щий от e), что дл€ всех членов последовательности с номерами n>N верно неравенство
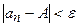 .
.
«аписывают это следующим образом: 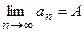 или a n Ѓ A при nЃ¥.
или a n Ѓ A при nЃ¥.
ѕоследовательность, имеюща€ предел, называетс€ сход€щейс€, в противном случае - расход€щейс€.
√еометрический смысл предела числовой последовательности состоит в том, что точки an, начина€ с некоторого номера n>N, лежат внутри интервала (A-e, A+e), т.е. попадают в какую угодно малую e-окрестность точки а.






