править]Гиперболические функции

Основная статья: список интегралов от гиперболических функций

также

также

Интегрирование методом замены переменной

Рассмотрим неопределенный интеграл F (x) некоторой функции f (x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой. Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.   6. Метод подстановки (замена переменной интегрирования) Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а) где – монотонная, дифференцируемая функция; б) – новая переменная. В первом случае формула замены переменной имеет вид: . (6.1) Во втором случае: . (6.2) В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.

Пример 1

Вычислить . Решение. Сделаем замену . Тогда . Следовательно, интеграл принимает вид

Интегрирование по частям

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

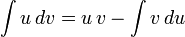
Доказательство

Функции и гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

§

§

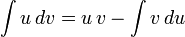
§ Иногда этот метод применяется несколько раз:

§ Данный метод также используется для нахождения интегралов от элементарных функций:

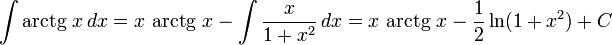
§ В некоторых случаях интегрирование по частям не даёт прямого ответа:

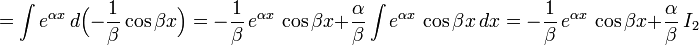
Таким образом один интеграл выражается через другой:

3. Интегрирование рациональных функций.

 

Функция называется рациональной, если ее можно представить в виде отношения двух многочленов. Например, если R (x) — рациональная функция одной переменной x, то

R (x) = am xm + am − 1 xm − 1 + … + a 1 x + a 0 bn xn + bn − 1 xn − 1 + … + b 1 x + b 0 ≡ Pm (x) Qn (x) .

Здесь, как обычно, индексы у P_m (x) и Q_n (x) указывают степени этих многочленов.

Многочлены являются рациональными функциями (у них знаменатели тождественно равны единице). Если рациональная функция не является многочленом, то она называется дробной.

Рациональная функция называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе и неправильной, если степень многочлена в числителе больше либо равна степени многочлена в знаменателе.

Правильную рациональную функцию одной переменной x можно единственным образом представить в виде суммы элементарных дробей

A (x − a) k , Mx + N (x 2 + 2 px + q) k (p 2 − q < 0),

где A, M, N, a, p, q — действительные числа и k — натуральные числа.

В этой сумме каждому действительному нулю a кратности k знаменателя Q_n (x) соответствуют k слагаемых

A 1 x − a + A 2 (x − a)2 + … + Ak (x − a) k .

Каждой паре комплексно сопряженных нулей кратности k знаменателя Q_n (x) (являющихся нулями квадратного трехчлена x ² + 2 px + q) соответствуют k слагаемых

M 1 x + N 1 x 2 + 2 px + q + M 2 x + N 2 (x 2 + 2 px + q)2 + … + Mlx + Nl (x 2 + 2 px + q) l .

Представление правильной рациональной функции в виде суммы элементарных дробей называется разложением на элементарные дроби.

Коэффициенты элементарных дробей, фигурирующих в разложении, однозначно определяются условием тождественности правильной рациональной функции и ее разложения.

Дробная рациональная функция

Рациональная дробь

3. Интегрирование простейших рациональных дробей.

4. Если дробь неправильная (т.е. степень P (x) больше степени Q (x)), преобразовать ее в правильную, выделив целое выражение;

 

5. Разложить знаменатель Q (x) на произведение одночленов и/или несократимых квадратичных выражений;

 

6. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

 

7. Вычислить интегралы от простейших дробей.

8. Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.

9. Доказательство.

10. Представим рациональную дробь в виде: 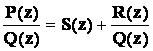. При этом последнее слагаемое является правильной дробью, и по теореме 5 ее можно представить в виде линейной комбинации простейших дробей. Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.

11.

12. Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.

13. Если P(z) и Q(z) – многочлены в комплексной области, то - рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.

14. Любую неправильную дробь можно представить в виде: ,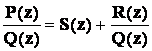

15. где

16. P(z) = Q(z) S(z) + R(z),

17.

18. a R(z) – многочлен, степень которого меньше степени Q(z).

19. Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как является правильной дробью.

20.

21. Определение 5. Простейшими (или элементарными) дробями называются дроби следующих видов:

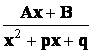22. 1) , 2) , 3) , 4) .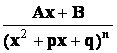

23.

24. Выясним, каким образом они интегрируются.

25. 1)

26. 2)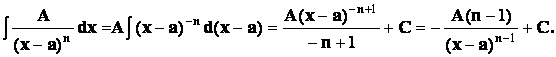

27. 3) (изучен ранее).

28.

29. Теорема 5. Всякую правильную дробь можно представить в виде суммы простейших дробей (без доказательства).

30.

31. Следствие 1. Если - правильная рациональная дробь, и если среди корней многочлена 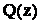будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:

32.

33.

34. Пример 1.

35.

36. Следствие 2. Если - правильная рациональная дробь, и если среди корней многочлена 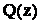будут только кратные действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го и 2-го типов:

37.

38.

39.

40.

41. Пример 2.

42.

43. Следствие 3. Если - правильная рациональная дробь, и если среди корней многочлена 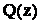будут только простые комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го типа:

44.

45.

46. Пример 3.

47.

48.

49. Следствие 4. Если - правильная рациональная дробь, и если среди корней многочлена 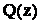будут только кратные комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:

50.

51.

52.

 

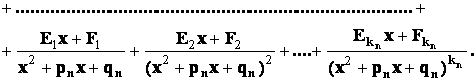
Разложение рациональных функций в сумму простейших дробей.

 

Интегрирование иррациональных функций,

Теорема Чебышева для интегрирования дифференциальных биномов