≈сли формулу зависимости измер€емых величин записать в линейном виде, то по графику можно определить некоторые еЄ параметры. Ќапример, чтобы получить из экспоненты пр€мую, нужно еЄ прологарифмировать. “ак, вместо  построим линейную зависимость
построим линейную зависимость 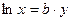 . “огда легко определить величину
. “огда легко определить величину 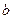 .
.
ƒл€ формулы  получаем величину
получаем величину  как отсечку на оси
как отсечку на оси  (где
(где 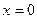 ) и тот же множитель
) и тот же множитель 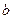 (рис.4). ѕоскольку экспериментальных точек много, берут дл€ расчЄта точки на пр€мой подальше друг от друга:
(рис.4). ѕоскольку экспериментальных точек много, берут дл€ расчЄта точки на пр€мой подальше друг от друга:

 (угловой коэффициент пр€мой)
(угловой коэффициент пр€мой)
–ис.4
≈сли экспериментальные точки не легли чЄтко на пр€мую, то дл€ определени€ углового коэффициента используют один из двух методов Ц метод парных точек или метод наименьших квадратов.
Ќа графике метод парных точек выгл€дит следующим образом (рис.5):
 –ис.5
–ис.5
Ќумеруют точки (на рисунке их 6), дел€т пополам (с 1 по 3 и с 4 по 6) и соедин€ют попарно, точку 1 с точкой 4, 2 с 5, 3 с 6. ѕолучаютс€ три пр€мые в данном случае. ќпредел€ют угловой коэффициент дл€ всех трЄх пр€мых и усредн€ют его. Ёто и есть искома€ величина 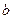 . ¬сЄ это не об€зательно делать графически, можно результаты измерений занести в таблицу в удобном виде. ƒл€ приведЄнного примера это будет выгл€деть так:
. ¬сЄ это не об€зательно делать графически, можно результаты измерений занести в таблицу в удобном виде. ƒл€ приведЄнного примера это будет выгл€деть так:
| Ќомера точек | 
| 
| ѕары точек
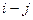
| 
| 
| 
|
 1 1
| 1-4 | |||||
 2 2
| 2-5 | |||||
 3 3
| 3-6 | |||||
 4 4
| ||||||
 5 5
| ||||||
 6 6
|
а дальше, поскольку получилось несколько значений 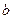 , вычисл€ем среднее и его погрешность, как дл€ многократных пр€мых измерений.
, вычисл€ем среднее и его погрешность, как дл€ многократных пр€мых измерений.
ћетод наименьших квадратов позвол€ет определить и  и
и 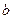 наилучшим образом. »х значени€ вычисл€ютс€ так, чтобы сумма квадратов отклонений измеренных значений от пр€мой была наименьшей.
наилучшим образом. »х значени€ вычисл€ютс€ так, чтобы сумма квадратов отклонений измеренных значений от пр€мой была наименьшей.
ѕриводим формулы дл€ расчЄта этим способом.
 ,
,  .
.
«десь и  и
и  - обозначени€ усреднЄнных величин.
- обозначени€ усреднЄнных величин.






