Главное свойство случайных величин: при повторных измерениях в одинаковых условиях их результаты меняются случайным образом. Распределение значений искомой величины 
можно увидеть, если построить гистограмму (Рис.1).
На горизонтальной оси откладываем измеренные значения . Интервал значений от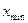 
до 
разбиваем на малые интервалы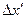 
. На вертикальной оси - отношение 
, где 
полное количество результатов, 
- их количество в каждом интервале . 
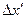доля результатов в данном интервале 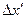, т.е. вероятность попадания в него результата отдельного измерения. имеет смысл некоторой плотности вероятности.
Рис.1
При очень большом количестве результатов, 
, гистограмма переходит в плавную кривую, тогда именно 
называют плотностью вероятности попадания конкретного результата в данный малый интервал 
. Другое название этой дроби – закон распределения, или распределение случайной величины.
Обычно совокупность результатов многократных измерений характеризуют двумя величинами – 1) среднее значение 
и 2) дисперсия 
, усреднённый квадрат отклонения данного результата от его среднего значения
.
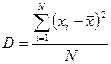Величину 
называют среднеквадратичным отклонением результатов наблюдений, т.е. 
.
При малом 
нужно использовать формулу 
, чтобы не получалась величина 
очень большой. (математически такая замена доказывается строго).
и характеризуют разброс результатов отдельных наблюдений около среднего значения.
