Наиболее часто применяемое распределение ошибок – нормальное, или распределение Гаусса. Предположения:
1) искомая величина может принимать непрерывный ряд значений от 
до 
,
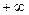2) центр распределения – одновременно его центр симметрии,
3) увеличению отклонения 
от центра соответствует уменьшение вероятности обнаружить его (
в данном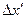 
.
Формула для распределения Гаусса 
.
Максимальное значение плотности вероятности 
. Зависимость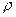 
от значения 
показана на рис.2:
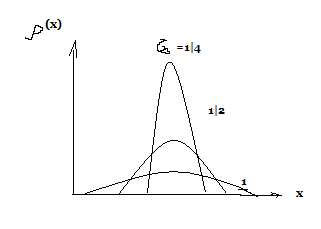Максимальное значение 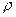соответствует среднему значению 
. Поэтому его называют наиболее вероятным значением измеряемой величины.
С увеличением увеличивается вероятность больших ошибок, а значит, уменьшается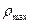 
. (
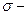разброс результатов).
Каждому распределению соответствует доверительный интервал (на рис. 3 от 
до 
), где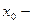 
произвольное отклонение от среднего значения . Его называют полушириной доверительного интервала.
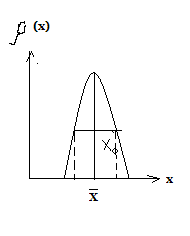
Рис.3
Интегралы от функции Гаусса 
для разных пределов интегрирования вычислены и представлены в справочной литературе. Они определяют вероятность попадания результата во всю область значений . Для области от до + 
интеграл равен единице (достоверный факт,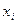 
в этом интервале есть).
Обычно распределение характеризуют не самой полушириной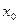 
, а относительной величиной 
. Именно она используется для определения погрешности многократных измерений. Вероятность того, что значение 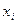попало в доверительный интервал, обозначают 
. Она называется доверительной вероятностью. В таблице для величин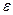 
указывается и . Так, при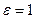 
, т.е. при 
, получается 
, т.е. 
результатов находится в доверительном интервале.
Наиболее часто используются значения 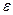, приведённые в таблице:
|
| |||
|
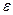
| 0,68 | 0,95 | 0,997 |
Для определения погрешности результатов многократных измерений используют не ошибку отдельного наблюдения, а ошибку среднего значения:
, тогда погрешность случайной величины 
и окончательный результат записывают в виде:
при 
,
где 
коэффициент Стьюдента, зависящий и от количества результатов и от доверительной вероятности (вычислены по законам теории вероятности). Его значения приведены в таблице 2 для наиболее часто используемых доверительных вероятностей. Выбор доверительной вероятности зависит от характера измерений. При обычных измерениях можно ограничиться , равной 0,9 или 0,95. Если требования к надёжности результатов предъявляются высокие, то выбирают 
Таблица 2
| |||||||||||
|
| 6,3 | 2,9 | 2,4 | 2,1 | 2,0 | 1,9 | 1,8 | 1,8 | 1,7 | 1,7 |
| 12,7 | 4,3 | 3,2 | 2,8 | 2,6 | 2,4 | 2,3 | 2,1 | 2,1 | 2,0 | |
| 31,8 | 7,0 | 4,5 | 3,7 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,4 |
