При численном решении краевой задачи теплопроводности температуру определяют в дискретных точках пространства и в дискретные моменты времени. Для задачи (1.1) – (1.4) неявная абсолютно устойчивая в счете безытерационная конечно-разностная схема имеет вид
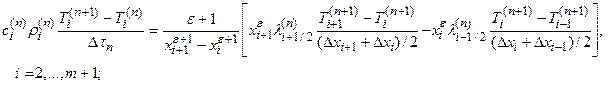(1.5)
(1.6)
(1.7)
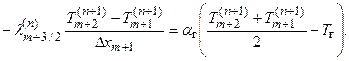(1.8)
Здесь предполагается, что геометрическая область, в которой ищется решение задачи (1.1) – (1.4), разбита на m слоев таким образом, что вектор нормали к границе каждого слоя коллинеарен орт-вектору оси Ox (см. рисунок 2). Через 
и 
обозначены координаты соответственно левой и правой границы i –го слоя. С целью распространения конечно-разностного уравнения (1.5) на крайние (2-й и m +1-й) слои области введены также два фиктивных (1-й и m +2-й) граничных слоя. Толщина каждого из фиктивных слоёв принимается равной толщине соответствующего прилегающего к нему слоя области, то есть 
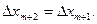Верхние индексы (n) и (n+1) обозначают два последовательных временных слоя 
и 
разделённых промежутком времени 
Температуры 
(i = 1, 2,…, m+ 2) определяются в серединах соответствующих пространственных слоев.
Плотность, теплоемкость и коэффициент теплопроводности рассчитываются в (1.5) – (1.8) следующим образом:
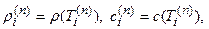
Отметим, что температуры наружной и внутренней поверхностей лопатки явно не присутствуют в уравнениях (1.5) – (1.8). При необходимости, на n -м временном шаге они могут быть определены по формулам
.
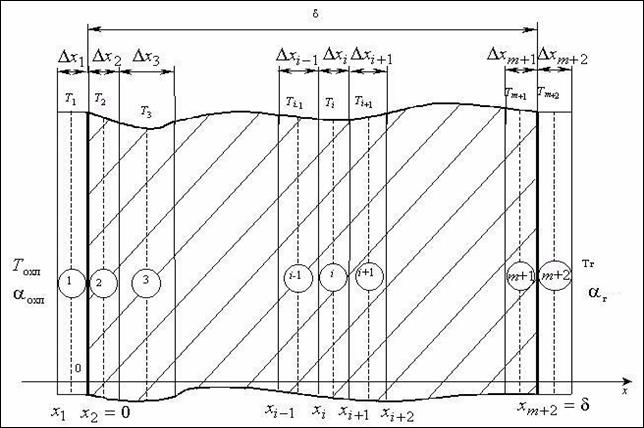
Рисунок 2 – Схема разбиения
