В отличие от дефлекторной лопатки, охлаждаемая матричная лопатка обладает более сложной геометрией поперечного сечения (см. рисунок 3), что обусловливает значительно большую неравномерность распределения температуры. Однако известно, что в большинстве случаев величины тепловых потоков по высоте лопатки отличаются незначительно и поэтому неравномерностью распределения температуры по высоте можно пренебречь. В этом случае задача исследования теплового состояния лопатки сводится к задаче нахождения двухмерного температурного поля в среднем сечении по высоте лопатки в каждый момент времени.
Будем предполагать, что температура газа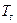 
и температура охлаждающего воздуха 
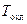не меняются с течением времени и одинаковы для любого участка профиля. Коэффициенты теплоотдачи от газа к лопатке 
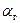и от лопатки к охлаждающему воздуху 
на каждом участке границы профиля также считаем постоянными и равными их соответствующим средним значениям на участке.
С учетом сделанных допущений распределение температуры по профилю лопатки будет удовлетворять следующей краевой задаче нестационарной теплопроводности:
(1.11)
(1.12)
(1.13)
Рисунок 3 – Профиль матричной лопатки охлаждаемой турбины
Здесь через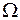 
обозначена геометрическая область, занятая профилем лопатки;
- искомая температура; 
- время, отсчитываемое от начала нагревания;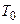 
- начальная температура лопатки; 
- граница i –го участка профиля, омываемого средой с температурой 
и характеризуемого значением коэффициента теплоотдачи 
; 
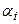- температура на границе i –го участка; I – число участков границы профиля.
Получить аналитическое решение задачи (1.11) – (1.13) в общем случае не представляется возможным, поэтому ее решение проводится численно, с использованием вычислительной техники. В настоящей курсовой работе для решения этой задачи используется метод конечных элементов.
