- угловая частота вращения вектора;
Сложение колебаний:
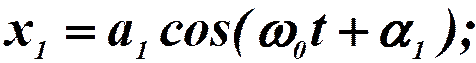
Результирующий вектор вращается с той же угловой частотой:
5. Затухающие колебания:
- коэффициент сопротивления;
- коэффициент квазиупругой силы;
- собственная частота системы;
Общее решение имеет вид:
и 
- постоянные;
Это гармонические колебания частоты 
с амплитудой, меняющейся по закону:
Скорость затухания колебаний определяется величиной, называемой коэффициентом затухания:
Найдем время 
, за которое амплитуда уменьшится в 
раз:
Отношение значений амплитуд, соответствующих моментам времени, отлич. От 
, равно:
Декремент затухания:
Логарифм декремента затухания:
Закон убывания амплитуды:
Добротность системы:
6. Вынужденные колебания:
- коэффициент затухания;
- собственная частота;
- амплитуда вынуждающей силы;
- частота силы;
Решение уравнения:
