1) Определение φ и u по измеренным зенитным расстояниям
cos z = sin φ sin δ + cos φ cos δ cos t и t = T' + u – a (1)
Если для двух (или более) светил, для которых по Астрономическому ежегоднику известны a и δ, измерены z (или h) по звёздным часам в момент времени T', то по (1) можно найти φ и u.
2) Определение φ и u в момент кульминации (t = 0 или 12h)
Для верхней кульминации к югу от зенита: φ = δ + z (2)
Для верхней кульминации к северу от зенита: φ = δ – z (3)
Для нижней кульминации: φ = 1800 – δ – z (4)
Т.о., по известному δ и измеренному z из (2) – (4) определяют широту
20.Методы определения координат и положений звёзд (a и d).
Абсолютные и относительные методы измерения экваториальных координат.
Измеряются зенитные расстояния (или высоты) незаходящей звезды в верхней и нижней кульминации:
z в.к. = δ – φи z н.к. = 1800 – φ – δ
Откуда: δ = 900 – ½ (z н.к. – z в.к.) и φ = 900 – ½ (z н.к. + z в.к.)
Т.е. определена широта места наблюдения и склонение одной звезды. Аналогичным образом находятся φ и δ для нескольких незаходящих звёзд, и значение φ усредняется. Далее по формулам (2) – (4) находятся склонения других звёзд (в т.ч. и заходящих).
Абсолютный метод определения прямых восхождений:
EE' – эклиптика, QQ' – небесный экватор
ε – наклонение эклиптики к экватору (угол между плоскостями)
mC – склонение центра Солнца δ● (дуга на поверхности сферы)
¡ m – прямое восхождение Солнца a●
Сферический треугольник ¡ mC – прямоугольный, поэтому:
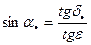
Вблизи дней солнцестояний (т.е. когда δ● принимает экстремальные значения) проводят измерения δ●, абсолютная величина которого = ε.
Далее вычисляется a● и s = a● = T' ● + u, т.е. поправка часов.
Выбираются 30 – 40 ярких звёзд, равномерно расположенных вдоль эклиптики и небесного экватора, и которые можно наблюдать до или после наблюдений Солнца. Такие звёзды называются часовыми.
При наблюдении часовых звёзд определяют их моменты прохождения через меридиан (кульминации): T' 1, T' 2, …, T'n.
При наблюдении Солнца определяется момент его прохождения через меридиан T' ● и зенитное расстояние в этот момент z ●. Далее вычисляется δ● и a●, а также поправки и ход часов на каждый день наблюдения.
Для каждого дня наблюдения составляют уравнения для Солнца и часовых звёзд: a● = T' ● + u, a1 = T' 1 + u 1, …, a n = T'n + un.
В уравнении для Солнца известны все величины, а в уравнениях для часовых звёзд – величины T'i и поправки часов: ui = u + ω(T'i – T' ●).
Т.о. можно определить прямые восхождения звёзд абсолютным методом:
a i = T'i + u + ω(T'i – T' ●).
В этом методе наблюдения Солнца необходимы для фиксации положения точки ¡ среди звёзд. С этой целью вместо Солнца можно наблюдать любую планету (в т.ч. и малую) Солнечной системы.
Относительные методы:
В относительных методах определение координат сводится к измерению разностей Δδ и Δa определяемых и опорных звёзд:
T – Ti = a – ai = Δai
z – zi = δ – δi = Δδi






