Определение 8. Множество, содержащее все свои предельные точки, называется замкнутым.
Определение 9. Множество, у которого все точки являются внутренними, называется открытым.
Определение 10. Совокупность всех точек прикосновения множества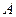 
называется его замыканием 
.
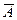Определение 11. Ограниченное замкнутое множество называется компактом.
Теорема (Больцано-Вейерштрасса). Всякое бесконечное ограниченное числовое множество имеет хотя бы одну предельную точку.
Доказательство. Пусть А – ограниченное множество, тогда существует такой отрезок [ c, d ], которому принадлежит А. Так как А – бесконечное множество, то хотя бы на одной из двух половин [ c, (c + d)/2], [(c + d)/2, d ] отрезка [ c, d ] имеется бесконечное подмножество множества А. Пользуясь этим очевидным предположением, отправляясь от отрезка [ c, d ] =∆1 с заданным на нем бесконечным множеством точек А, построим систему вложенных отрезков ∆ n, где каждый последующий отрезок составляет половину предыдущего и несет на себе бесконечное подмножество множества А. По принципу Кантора у этой системы есть общая точка х 0, докажем, что она является предельной для множества А. Возьмём любой интервал V с центром в точке х 0 ,скажем, длины σ >0. Пусть n таково, что длины отрезка ∆ n меньше σ /2. Включая в себя точку х 0, он целиком содержится в интервале V. Вместе с отрезком ∆ n в интервал V попадет бесконечное число точек множества А. Следовательно, х 0 есть предельная точка множества А, что и требовалось доказать.
Эта теорема также выражает принцип полноты числовой прямой, как и леммы Коши-Кантора и Бореля-Лебега.
